11.1 Overview
Logistic regression is the classic, historically prior classification procedure. The machine learning analyst, however, typically explores many alternatives in pursuit of optimal predictive accuracy. With modern computing power, we can experiment with various estimation algorithms, model types, and parameter settings, even for large data sets.
Another widely-employed classification procedure is the decision tree, which, as with logistic regression, can be applied to a classification target variable with two or more classes (labels, levels, values, groups). A decision tree provides a sequence of classifications.
Decision tree: Hierarchical structure of binary decisions.
The process of obtaining the hierarchical structure begins with all of the data and then successively divides the data into more homogeneous groups.
Each binary decision follows from a cutoff value for a feature variable. Prediction examples (instances, samples) with a value larger than the cutoff value into one group, and classify examples with a value less than the cutoff into another group. For example, given the amount of credit card debt as a percentage of income, classify all bank customers with a debt above a certain threshold as rejected for a loan and all customers with a debt below that level as accepted for a loan.
In practice, other variables would also be considered in the final decision for providing or not providing a loan. After the first binary decision, usually, introduce a subsequent decision based on a threshold of a second variable. A sequence of questions results expressed as If-Then rules that, when followed to the end, results in a classification of a given example to one group.
11.2 Example
To illustrate the process of forming a decision tree, return to our (real) data set of an online clothing retailer that predicts a customer as a man or a woman from their physical measurements. Consider the simpler analysis that relies upon only two features, the predictor variables: hand size and height. Figure 11.1 provides the scatterplot for 340 (actual) customers, with men’s and women’s measurements represented by different colors. With this scatterplot, explore the possibility of predicting man/woman from body measurements.
To accommodate some over-plotting due to the limited number of unique values for the measurements of height and hand size, plot points with partial transparency. However, this adjustment does not fully address the problem because points of different colors can also plot to the same coordinate. When points of only the same color over-plot the same coordinate, the exact number of such over-plots cannot be determined from the graph. Still, the plot serves as a helpful guide to how the decision tree algorithm defines regions of points based on homogeneity.
According to Figure 11.1, the potential for classification from these measurements appears realistic as male and female measurements generally cluster into different areas of the scatterplot. Males tend to the upper-right, and females tend to the lower-left. Given this differentiation, an efficient classification algorithm would generally obtain a successful classification.
The decision tree algorithm proceeds by considering all of the data and then determines the features from which to split the examples into two groups to obtain the maximal homogeneity (sameness) within each group. For this application, derive one group with the proportion of men as high as possible, and a second group with the proportion of women as high as possible.
Evaluate the various proposed splits at each step in the construction of a decision tree model with a homogeneity index. At a given node, everyone in the same class, such as Male or Female, yields a perfectly homogeneous group.
Gini impurity (applied to decision trees): Index of the impurity of a split, which varies from the desired 0 for perfect homogeneity (equality) to maximum inequality at 1, which indicates a random distribution of the data values across the groups.
The closer the Gini index to zero, the better. A Gini index of 0.5 denotes equally distributed elements across the groups, that is, the classes. For example, as shown in Figure 11.3, the Gini impurity of the initial or root node of 170 Females and 170 Males is 0.5.
For example, to classify a customer as a man or a woman from physical dimensions such as hand size and height, first classify each individual instance (or sample) according to their hand size as likely male or female. Given the resulting two sets of classifications, then according to height, further partition the derived two groups. The ideal solution, rarely obtained with real data, would consist of a sequence of decisions that lead to only male body types or only female body types, that is, perfectly homogeneous groups, without overfitting the tree to the data.
The Gini index is the default homogeneity index for Python’s sklearn machine learning framework. The estimation decision tree algorithm chooses the split that maximizes the drop in the Gini index. Although the estimation algorithm proceeds by choosing decisions that minimize Gini impurity, evaluate the ultimate fit of the model according to the resulting confusion matrix of true and false positives and true and false negatives, as shown below.
11.2.1 Split #1
For a given set of data, examine each feature one-by-one. The decision tree algorithm identifies each feature’s optimum value that splits the data into the most homogeneous groups.
Decision boundary: Value of a feature variable chosen that splits the values of the variable into two subsets.
Given the possible splits for all the features, the algorithm chooses the one split that yields the most homogeneity among the various groups.
The competition between the features yields hand size as the winner, the feature with a cutoff value that yields the most homogeneous groups. The first split from the decision tree algorithm identifies the following decision boundary:
- Female with hand size < 8.125
- Male with hand size \(\geq\) 8.125
The decision tree model with a single split of the data provides a simple prediction: Predict Female if hand size is less than 8.125, and predict Male otherwise.
For the first node, the estimation algorithm considers all the data to derive the evaluation of the first split.
root: The node at the top of the inverted tree structure indicates the first split, on all the data.
The basis for the chosen split follows from the structure of the data shown in Figure 11.2. The estimation algorithm selects the value of 8.5 for hand size, which divides the men and women as effectively as possible for these two groups. The group consists of mostly brown points (males) are on the right side of the line, and mostly blue points (females) on the left.
The resulting output of the decision tree algorithm for this single binary split at a Hand circumference of 8.125 inches appears in Figure 11.3. The root node begins with all 340 samples, 170 females and 170 males, so the Gini Coefficient is 0.5. Each tree node presents the corresponding prediction. This simple decision tree only has a depth of 1, so temporarily, until the tree expands to more depths, the bottom two nodes are leaves, nodes at the bottom of the tree.
For the first node, given the even split of Male and Female samples, because F precedes M in the alphabet the algorithm arbitrarily predicts Female, which signifies Female as the True value of the subsequent split. Also, because of the alphabetical ordering, by default, to define the reference group the dummy variable conversion arbitrarily leaves out the first group.
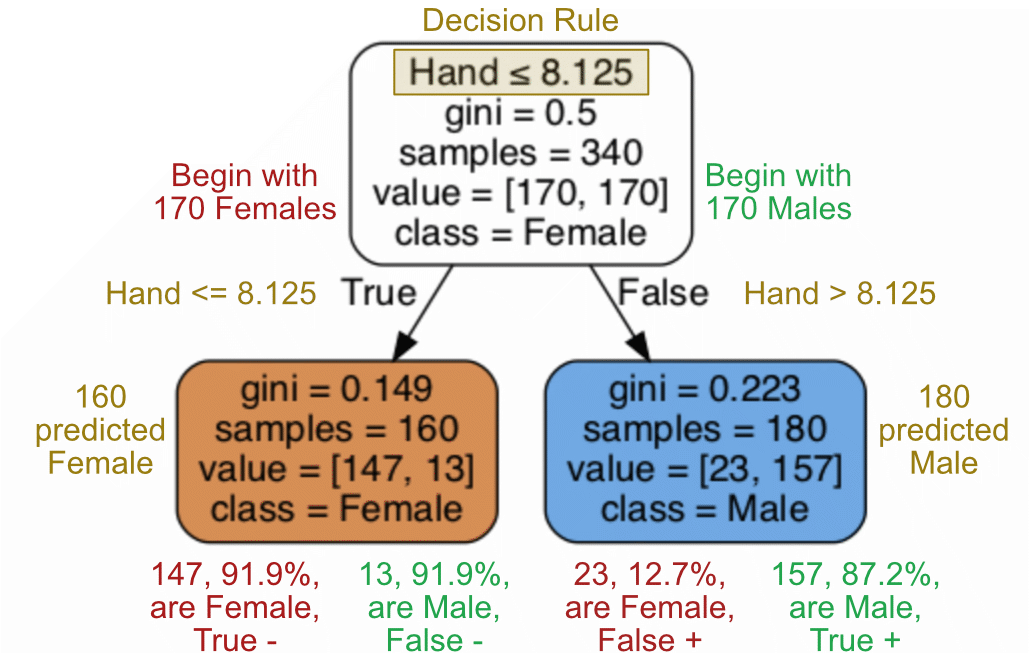
Interpret a decision tree, such as in Figure 11.3, according to the following rules.
- The decision rule is listed at the top of each node that is not a leaf (bottom row). The decision for each sample at that node follows from the specified cutoff value of a single variable.
- The bottom row of the tree, the leaves, do not have a decision rule. Instead, the leaves represent the predicted label, the final classification into one of the two groups or classes.
- If a sample satisfies the decision rule at a node, classify the sample by following the left arrow that branches from the node. Otherwise, follow the right-arrow branch.
- Read class= as predicted class=, the model’s classification for all of the samples located at that node.
- The prediction for the class at any node is the group with the largest number of samples at that node.
- Each value has two entries. The entry on the left is the number of samples in the predicted class of the root node, the direction of the left-arrow branch.
- The four values resulting from the two nodes that split off their shared parent node specify the number in each of the following groups: True +, True -, False +, False -.
- The intensity of the color for each node in the decision tree indicates the extent of correct classification in terms of the Gini Coefficient. More saturated color indicates a lower Gini, so more confidence in the classification.
How accurate are predictions with this simple decision tree model with only one decision rule? The confusion matrix in Table 11.1 follows from this simple classification rule based on Hand size, all values of the matrix taken from the temporary leaves of the decision tree in Figure 11.3.
| actual | pred F | pred M |
| F | 147 | 23 |
| M | 13 | 157 |
The result of this first split at a Hand circumference of 8.125 inches is the Female group with 147 females and 13 misclassified males. The corresponding Male group has 157 males and 23 misclassified females. This single split decision tree model resulted in a classification accuracy of 89.4%.
\[ \mathrm{accuracy=\frac{true \; positives + true \; negatives}{all \; outcomes}=\frac{147 + 157}{147+13+157+23}=0.894}\]
Will additional complexity improve the predictive efficiency of the model? For a decision tree model, add complexity with an additional split of each of now two groups from the first split.
11.2.2 Split #2
The first split to obtain the decision tree model in Figure 11.3 partitioned the complete data set into two groups, represented by the points to the left of the vertical line in Figure 11.2, and the right of the line.
This first split resulted in a tree of one-level depth.
Tree depth: The number of If-Then statements evaluated before classifying an example (instance, sample) into one of the criterion groups.
To obtain a more complex model with two levels of depth, apply the same logic from the first split, but now separately applied to each partition. Repeat this process for each existing data partition, of which only two partitions exist after the first split.
First, consider the data partition to the left of the vertical line in Figure 11.2, that is, predict Female. Where to place a horizontal line representing height that divides only that set of partitioned data into maximally homogeneous groups? Find more blue points toward the bottom of the partition and more brown points at the top. Figure 11.4 displays the resulting horizontal line computed by the decision tree algorithm for a height of 69.5 inches.
Apply the same logic to the second partition of data, those points to the right of the vertical line in Figure 11.2 and Figure 11.4. In this partition, the horizontal line is lower than for the first partition to more effectively separate the blue points at the bottom of the partition from the brown points. Figure 11.5 illustrates this decision boundary for a height of 65.5 inches.
From these partitions, create the decision tree for this two-depth model shown in Figure 11.6. Again, lighter shades indicate a greater percentage of mis-classifications.
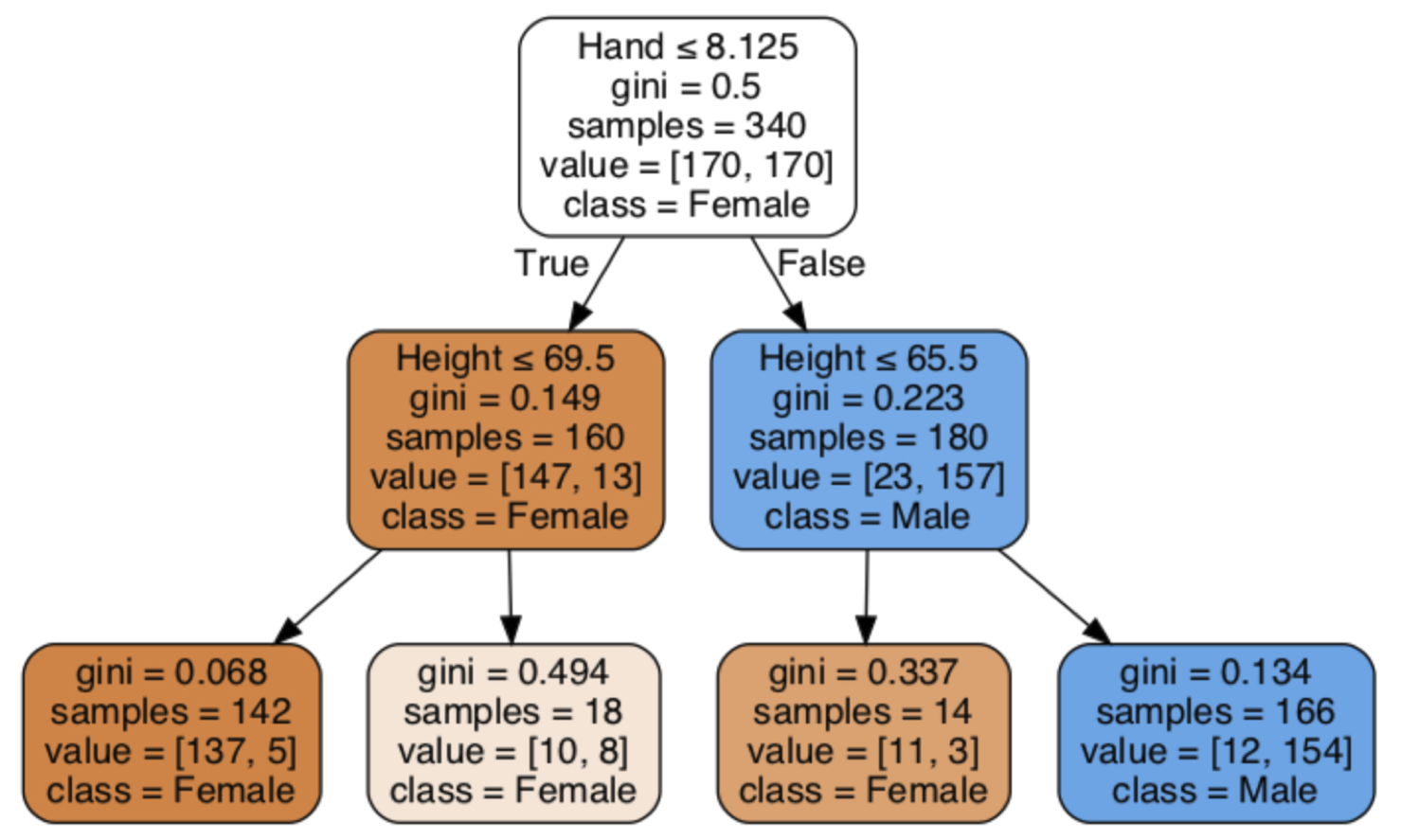
At the second level of depth, find only one node that predicts Male, the node on the extreme right. The two sequential decision rules that predict Male for this node begin with all customers in the data set with a hand size greater than 8.125 inches, and then from those 180 customers, the 166 customers with a height greater than 65.5 inches.
leaf: A node at the bottom of the decision tree, which no longer splits, the final level of grouping.
The remaining three leaves predict Female. The leaf with the lowest percentage of misclassifications for all the leaves is at the extreme left in Figure 11.6. The decision rules correctly classify 137 of the 142 customers, with a hand size less than or equal to 69.5 inches and a height less than 69.5 inches, as Female. Accordingly, that leaf has the lowest Gini index of 0.068.
The leaf second from the left in Figure 11.6, which corresponds to the partition at the top left of Figure 11.5, provides the least accuracy. Customers with a hand size less than or equal to 8.125 inches yet are taller than 69.5 inches are almost evenly split between Female and Male. The slight tilt toward Female, 10 females versus 8 males, results in a prediction of Female for those customers. From a decision making perspective, the application of the model might avoid predicting Gender for tall customers with smaller hands, returning the result of Undecided. The machine learning analyst should evaluate if the information provided by additional body measurements provides information that more reliably distinguishes between males and females in this group.
The correct and incorrect classifications for the leaves in Figure 11.6 provide the information needed to generate the resulting confusion matrix. The total mis-classification of Male for predicted females is \(5 + 8 + 3 = 16\), the total number of false negatives as gathered from the three most left-ward leaves. The one leaf for predicting males indicates 12 mis-classifications, false positives. Table 11.2 presents the complete confusion matrix.
| actual | pred F | pred M |
| F | 158 | 12 |
| M | 16 | 154 |
From the confusion matrix, the computation of accuracy quickly follows.
\[ \mathrm{accuracy=\frac{true \; positives + true \; negatives}{all \; outcomes}=\frac{158 + 154}{158+16+154+12}=0.918}\]
The second split increased accuracy by more than 2% points. Will a third split accomplish the same or more?
11.2.3 Split #3
The third data split returns to the feature hand size to further partition each of the four partitions. Focus on the top-left partition that yielded 10 females and 8 males for the second level split, which is further partitioned for the third level as shown in Figure 11.7.
Further considering hand size, the algorithm partitions the three Female points with a hand size below 7.75 inches. A new leaf, at the third level, contains those three correct Female classifications. The remaining confusion centers on the remaining 15 people from that original partition, seven females and eight males, as illustrated in the tree diagram in Figure 11.8, and also the corresponding shaded partition from the third split in Figure 11.7. The confusion in this remaining group consists of taller customers with a hand size just slightly lower than the threshold from the original hand size decision boundary.
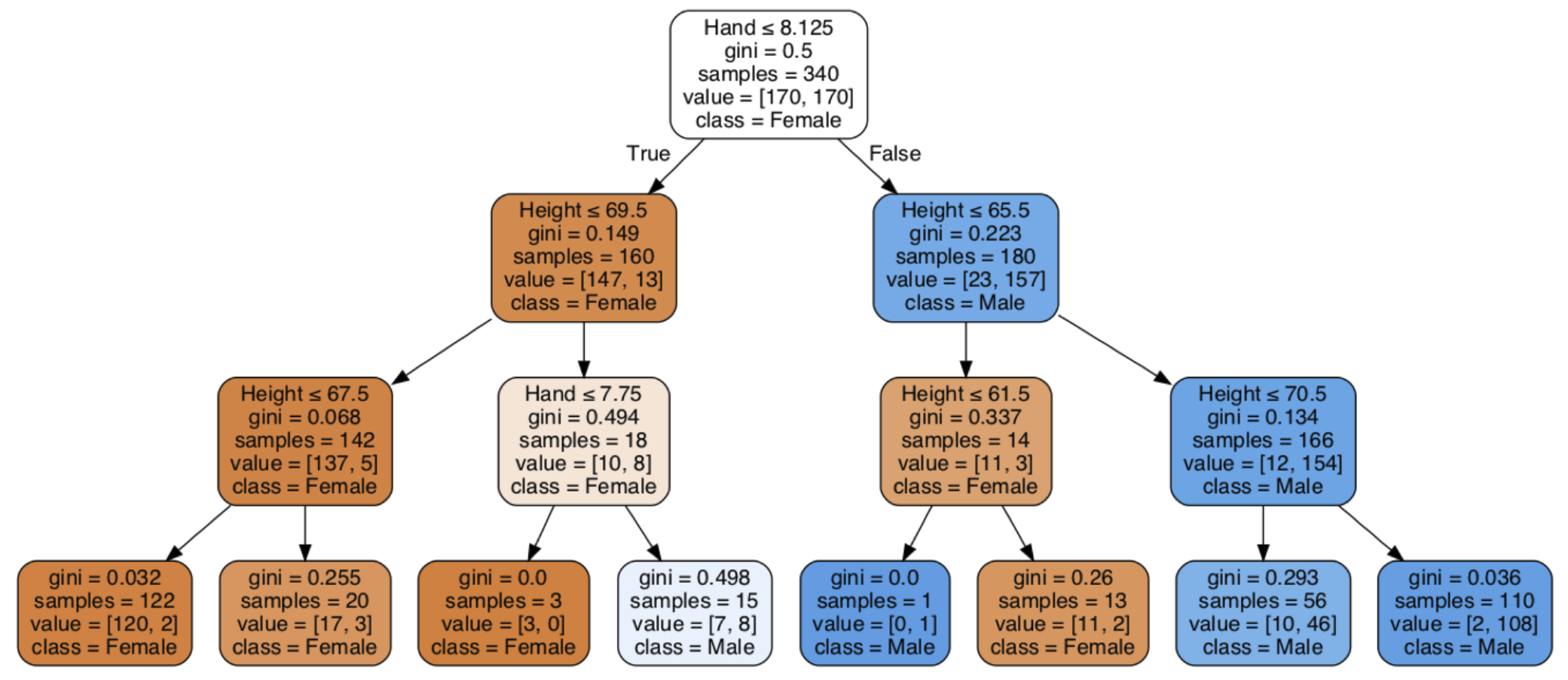
Construct the confusion matrix from the information in now the \(2^3=8\) leaves. The three male leaves on the right have a total of 12 misclassified females, false positives in this context. The leaf with the most confusion, seven females and eight males, contributes another 7 false positives, for a total of 19.
Table (tbl:cm3?) presents the full confusion matrix for evaluating this three-level decision tree.
| actual | pred F | pred M |
| F | 151 | 19 |
| M | 7 | 163 |
Computation accuracy as follows.
\[ \mathrm{accuracy=\frac{true \; positives + true \; negatives}{all \; outcomes}=\frac{163 + 151}{163+7+151+19}=0.924}\]
Accuracy increases only slightly from the two-level tree, a proportion of 0.06. The slight increase in accuracy is accompanied by a decrease in sensitivity (recall), with 12 false positives for the two-level tree and 19 false positives for the three-level tree. In this context, the two-level tree would generally be preferred.
11.3 Overfitting
A decision tree model with three levels of depth did not improve the two-level model. What happens as the model becomes more complex as more levels are added? Is there some advantage? The answer is no.
As discussed in Section (ch:predict?), the training data fit can be too good, the estimated model can overfit the data. As the model is revised to become increasingly complex, there are more opportunities for the learning algorithm to properly account for all males and females from their respective body measurements in this specific data set.
With sufficient complexity, a model can achieve perfect prediction on the training data by modeling idiosyncratic sampling error.
The ability of the derived decision rules to classify perfectly from the training data is of no practical consequence because the model already knows the correct classification of each person in the training data.
What happens when the complexity of the decision tree model for the Gender prediction analysis grows to 10 splits? The result is an overfit model, illustrated in the following table for a 5-fold cross-validation. Training data accuracy, listed in the column train_accuracy, for each of the five splits assessed by the Gini coefficient, is perfect. The 10-split model perfectly classifies male and female body types in the training data.
The difficulty is that true predictive accuracy, here labeled test_accuracy, averages 0.891 over the five splits, less than the 0.921 for the two-split model. Moving from two to 10 splits worsens predictive fit instead of improving fit.
fit_time score_time test_accuracy train_accuracy test_recall \
0 0.004 0.009 0.882 1.0 0.889
1 0.003 0.004 0.882 1.0 0.842
2 0.004 0.006 0.941 1.0 0.933
3 0.002 0.004 0.897 1.0 0.889
4 0.002 0.004 0.853 1.0 0.833
train_recall test_precision train_precision
0 1.0 0.889 1.0
1 1.0 0.941 1.0
2 1.0 0.933 1.0
3 1.0 0.914 1.0
4 1.0 0.833 1.0 Although overfitting with a too complex model is the more general problem, consider its opposite, underfitting. In this example, the decision tree with just one level of fit did not match the tree’s performance on the testing data with a depth of two. The one-depth model that underfits the data is too simple. As always, a primary challenge in building machine learning models seeks the optimal balance between underfitting and overfitting. As previously stated, the best model achieves parsimony. For a given data set, the model should be as simple as possible without sacrificing fit but no simpler.
11.4 Hyper-Parameter Tuning
11.4.1 Parameter vs. Hyper-parameter
What does the machine learn in an application of machine learning? The chosen estimation algorithm estimates the values of the model’s parameters from the training data. An example of such parameters are the linear weights of the features in a linear model, the \(b_i\). Another example is the split at each level implemented by the decision tree algorithm.
Model parameter: Value estimated from the data that defines a specific model, what the machine learns.
Fit a specific linear model that predicts a value of \(y\) to the data to estimate the values of its parameters, the \(y\)-intercept and the slope coefficient for each feature or predictor variable. Fit a specific decision tree to the data to obtain the tree structure that labels a value of \(y\).
However, the analyst sets other characteristics of the model.
Hyper-parameter: A characteristic of the model set by the analyst before learning begins.
The machine learns the values for the model’s parameters that optimize fit. However, each specification of the model represents a specific combination of the values of the more general hyper-parameters.
Hyper-parameters for decision trees include the number of features evaluated at each node and the maximum depth of the resulting decision tree. Each value of a hyper-parameter defines a specific model, such as a tree depth of four versus a tree depth of five. The learning algorithm then estimates the values of the parameters present in that specific model. Investigating these questions results in another set of more general characteristics regarding each model for which the machine learns the values of the model’s parameters. We can systematically explore combinations of different hyperparameters by evaluating the fit of each resulting model to help choose the best form of the model.
11.4.2 Grid Search
The Python sklearn environment provides a formal procedure for the ultimate fishing expedition, a data scientist’s dream expedition. The sklearn machine learning framework provides for systematically investigating how a class of related models perform in terms of predictive efficiency for all possible combinations of different values of hyper-parameters. For example, how is classification accuracy affected by moving from a depth of three levels to four levels? Do five features increase classification accuracy with more than three features?
Efficient analysis of the impact of different hyper-parameter values on model fit systematically changes their values and evaluates the corresponding predictive accuracy of the resulting models.
Grid search: Investigate the performance of related models by systematically changing the values of hyper-parameters.
Adding a grid search to an analysis defines the following progression for doing supervised machine learning:
- Especially if a large data set constrains machine time, begin with a single training/test split of the data to understand if the model appears to have some validity.
- If promising, generalize this single split for that model to a \(k\) splits with a \(k\)-fold cross-validation of \(k\) training/testing splits.
- Generalize beyond the single model with a grid search in which each model configuration, such as a specific combination of tree depth and number of features, is analyzed with its own \(k\)-fold cross-validation.
The only downside to this grid search procedure is computer time, which is generally of consequence for massive data sets. Exploring two hyper-parameters with five different values yields \(5*5=25\) different models to investigate. Also, consider the desirable cross-validation. Five cross-validations of each combination of the five levels of the two hyper-parameters result in \(5*5*5=125\) separate analyses. The advantage is that the analyst can examine the five analyses of fit for each of the 25 models and then choose the best model in terms of the optimal combination of model and parsimony.
Pursuing the best alternative minimizes the prediction error from applying a model estimated from training data to new testing data. A warning from traditional statistics is to refrain from embarking on these fishing expeditions, more or less randomly searching for the best-fitting model. That warning is real, but only when the same data are continually re-analyzed or other characteristics of the data are transferred to the testing data.
Data leakage: Characteristics of the data used to train the model inadvertently influence the testing data on which the model is evaluated.
A proper machine learning analysis avoids data leakage to ensure to always test the model on new data entirely separated from any influence of the training data.
The most apparent form of data leakage evaluates model fit on the data in which it was trained. More subtle influences also are possible. For example, standardizing all of the data before splitting into training and testing sets results in the both data sets sharing data with the same metric. More properly, standardize the training and testing data separately.
The good news is that if we avoid data leakage, we can “fish” as much as we wish because any chance optimization on the training data by definition does not generalize to testing data. To our benefit, sklearn makes this fishing expedition easy. The application of machine learning does not apply newly discovered laws of statistics. Instead, it relies upon access to modern computing power to accomplish analyses that were either impossible or impractical in earlier times.
11.5 Random Forest
11.5.1 Decision Tree Overfitting
Decision trees provide one of the most interpretable models in machine learning. Statistical knowledge is not required to understand and apply a specific decision tree. Unfortunately, decision tree models tend to overfit, to have poor performance on the new data needed for prediction. Accordingly, the models tend to be somewhat unstable, to have high variance, which means much different models generally result from relatively small changes in the data.
Local optimization: Iterate with gradient descent to a solution by optimizing the consequences of the decision at each step of the process without referencing the best, overall global solution.
The decision tree solution follows local optimization. The problem is that there is no guarantee that optimizing each step of the iterative solution process provides the best possible overall solution.
Suppose one feature barely provides more homogeneous groups at the chosen decision boundary than does a second feature. Also, suppose that the second feature, if it had been chosen, would eventually lead to a decision tree that provides a more homogeneous solution in the leaves than for the solution obtained after choosing the first feature. The decision tree algorithm always selects the following feature and associated decision boundary only regarding optimization at each decision boundary. There is no global consideration at any point in the process of obtaining the entire solution from root to leaves.
A new type of estimation algorithm was developed to address this short-coming of decision trees and other machine learning procedures.
11.5.2 Ensemble Methods
To address the dual issues of increasing predictive power while avoiding overfitting, build a predictive model based on many different models that train on different random subsets of the data.
Ensemble model: Combine the results of randomly selected component models that are learned on different random subsets of the data to form a more robust predictive model.
Instead of relying upon a single model for predictions, combine multiple predictive models into a more general model based on the separate evaluation of each model.
The more general model acts as a manager, a collective intelligence. The input to the more general model are the predictions of the component models. Each component model has its advantages and disadvantages. The manager model evaluates each component model’s prediction for each data example and then learns which component performs the best in a given situation. Particularly when the component models disagree, the general model learns to optimally choose between the competing predictions, to predict from a collective consideration of their individual predictions.
Ensemble methods produce the most accurate predictive models and tend to overfit less. Hence, they are relatively robust to small changes in the data. In an ensemble of separate predictive models, the models compensate for each other’s limitations, with the result that the ensemble more readily achieves more accurate prediction than any of the constituent models.
11.5.3 Random Forest Classifier
The current state of predictive modeling is dominated by successful ensemble models that typically outperform a single predictive model, including decision trees. A decision tree is a single tree. A random forest is a forest of trees.
Random forest classifier: Constructs a series of decision trees where each tree is based on a different random sample of (a) the data, with replacement, and (b) the available features, with the classification of an example the result of the majority vote from the different trees in the forest.
Each individual decision tree in the forest is constructed from a random sample of the training data and a random sample of the features from which the classification is constructed. Each tree is constructed from different information.
Each decision tree yields its own predicted classification, the label, from each set of the values of the features, the predictor variables.
Bagging: A machine learning technique for reducing the variance of a model by integrating multiple models trained on distinct data samples.
Bagging is the process of generating multiple models, each with a subset of the data and potentially a subset of features, and then combining them to produce a more robust model less prone to overfitting. The result is a procedure that typically returns a higher level of classification accuracy than a single decision tree.
However, a random forest does not produce a single decision tree that explains how the prediction is obtained. Instead, the result is an integration of the output of many different trees. Obtain enhanced predictive ability at the expense of easy interpretability .