
❝ Prediction is difficult, especially when dealing with the future ❞
1.1 The Machine
The ability to predict the unknown is a skill in demand. To make effective decisions today, managers need to know what will likely happen next week, next quarter, or next year. The better we predict, the better we plan, and the better to prevent problems from occurring. The predicted variable could be inventory level for a particular SKU, mortgage interest rate, shipment time, demand for a product, customer churn (loss), housing prices, clicking on a web page ad, employee turnover, population size, percentage of quality shipped parts, and many, many other possibilities.
The basis for prediction? One approach predicts from a time series, previous values of the variable that together are used to predict a future value of the same variable. Another approach, discussed here, is to learn how other variables with known values relate to the variable of interest with the unknown value. The intrigue is that a machine can now learn these relationships.
A machine? The word machine applied here is a trendy, almost cute, but effective reference to programmed instructions running on a computer.
Machine: A computer that invokes a procedure according to pre-programmed instructions to accomplish a given task, such as learning.
People have always learned. Now machines can learn.
As applied here, learning proceeds from searching for patterns of related information from many existing examples of data. Except instead of you searching for these patterns from the data, the machine does the searching. And guess what? Given its staggeringly massive superiority in data processing speed, the machine uncovers many patterns much more effectively than can people. That is why we seek the machine’s help.
Machine learning: Instruct the machine to identify patterns inherent in data.
For example, the photographs stored on your phone are stored as digital data. As your phone’s computer searches your stored photographs to find those that contain you, the color of your hair helps distinguish you from your friend. Or, your phone’s computer searches your stored photographs for text, encodes the text as actual text as if you had typed it, and then indexes your photographs accordingly.
1.2 Prediction Equation
1.2.1 Models
Pattern recognition applies to many types of analyses. One application predicts the unknown. Predict, for example, a person’s unknown height from their weight, albeit, imperfectly. These discovered relationship patterns enable a specific type of machine learning.
Supervised machine learning: Methods to develop the best possible prediction of an unknown value of the relevant variable from the related patterns with known values of other variables.
The machine expresses its learning as one or more equations that transform the related information into a prediction.
Model: One or more equations that computes an unknown value of a variable from the values of other variables.
The most straightforward prediction follows from a single equation.
The model transforms a set of entered numeric values into a predicted value, as illustrated in Figure 1.1.

To apply the model, enter the related information, then compute the predicted value.
1.2.2 Example
Consider an online clothing retailer who must correctly size the garment for a customer not present to verify fit. Returns annoy the customer and vaporize the profit margin for the retailer. Unfortunately, the customer sometimes omits from the online order form crucial measurements needed to fit a garment properly. If the customer omits their weight, the retailer wishes to predict this unknown value from the measurements the customer did provide.
Both a person’s height and chest size relate to their weight. Leveraging these relationships, the retailer’s analyst first specifies a general form of the model. One popular choice is a model defined as a weighted sum of the variables, here height and chest size, plus a constant. What are the weights in the weighted sum that optimize the predictive accuracy of a customer’s weight? That discovery is the machine’s job.
For simplicity, this initial model derived from the data analysis in this example applies only to their male customers, the predominant customer type for this retailer.
\[\textrm{Predicted Weight} = 3.80(\textrm{Height}) + 7.32(\textrm{Chest}) - 386.22\] From examining the data values for each male customer’s recorded height, chest size, and weight, the machine learns the underlying weighted sum relationship. The machine estimated values of 3.80 and 7.32 for the respective weights of the two variables, plus the constant term of -386.22.
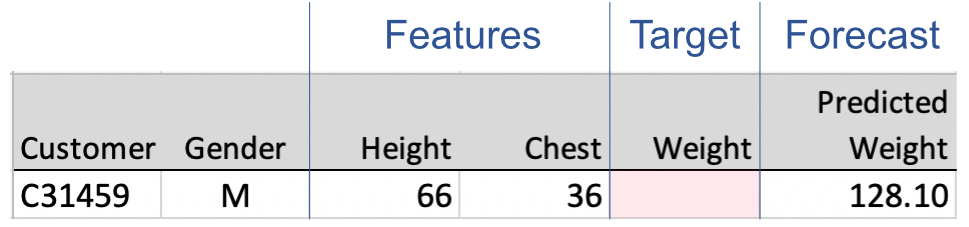
To apply the machine’s prediction model to a specific customer’s height and chest measurements, enter the corresponding data values, the measurements, into the prediction equation in place of the variable names. Suppose the customer reports a height of 68 inches and a chest measurement of 35 inches, illustrated in Figure 1.2.

From each specified entered value for every input variable in the model, the prediction model calculates a specific number, the prediction. The anticipated weight for a person 66 inches tall with a chest measurement of 36 inches is 128.10 pounds.
1.3 Variables
The analysis begins with the choice of the variable for which to predict an unknown value.
Target: The variable with the values to predict.
Generically refer to the target variable as \(y\), which assumes a specific variable name in a specific application, such as customer weight in the previous example. In traditional statistics, refer to the same \(y\) as the response variable or dependent variable, among other names.
From what information does the prediction of the value of the target, \(y\), proceed? In the online clothing retailer example, enter a customer’s height and chest size into the model.
Feature: One of the one or more variables from which to predict the value of the target variable.
Generically refer to the variables from which to compute the prediction as \(X\), uppercase to denote that typically \(X\) consists of more than one feature: \(x_1\), \(x_2\), etc. Traditional references to the \(X\) variables include predictor variables, independent variables, or explanatory variables.
The variables of interest for supervised machine learning models span a wide variety of applications. Table @ref(tab:regexamples) lists some business scenarios, each with three features. Some of the target variables are continuous, measured on a quantitative scale. The values of other target variables in Table @ref(tab:regexamples) are labels, where each label defines a single category.
| y | x1 | x2 | x3 | |
|---|---|---|---|---|
| Continuous Target | ||||
| shipment | ship time | distance | carrier | modality |
| product | sales | discount % | radio ads | online ads |
| county | housing starts | interest rate | county population | average income |
| adult | weight | height | chest | neck |
| employee | salary | experience | department | gender |
| magazine | ad cost | audience size | percent male | median income |
| Categorical Target | ||||
| customer | stay/churn | tenure | total charge | payment method |
| part | accept/reject | length | finish | shift produced |
| web ad | click/ignore | gender | age | time on page |
| youtube video | watch/ignore | political affiliation | age | recently watched |
For a continuous target variable, predict a value that is as close to the actual value as possible. When that actual value becomes known, assess how close the predicted value is to the actual value. For labels, prediction is classification into the correct category. The many applications of machine learning for both continuous and categorical target variables contribute to its increasingly widespread use.
1.4 Data
The data for analysis encapsulate the experiences from which the machine learns. Gather data for all the variables in the model. To prepare for computer analysis, organize the data into a table, such as in Figure 1.3, perhaps using a standard worksheet app such as Microsoft Excel, or the free and open-source LibreOffice Calc. List the data values for each variable in a single column. List the data values for each example in a single row.
Example: A row of data that contains the data values for the variables in the model for a specific person, company, region, or whatever the unit of analysis.
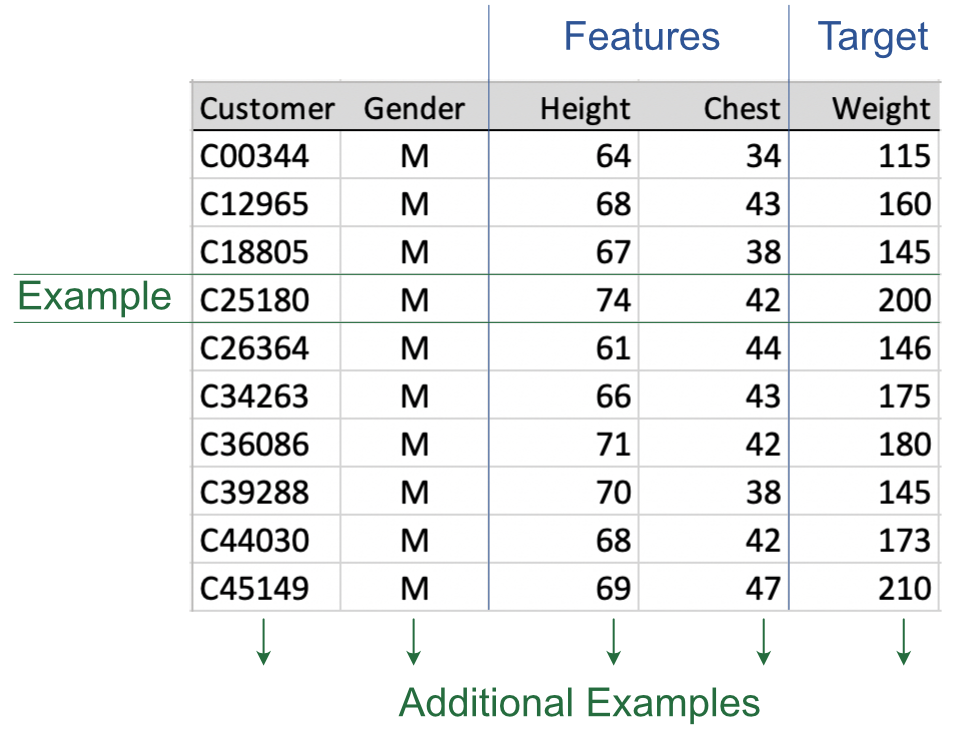
The ten rows of data shown in Figure 1.3, one row per customer, are illustrative only. In practice, the machine learns from many more examples. Be aware that the language that describes the data table is not always consistent. Other names for a data example, a row of data in a data table, include sample, instance, observation, and case.
After reading the data into your preferred machine learning application, such as the open-source and free R or Python, estimate the model with a machine learning algorithm. From the data, the (estimation algorithm implemented on the) machine learns the relationship between the \(X\) variables and the known values of \(y\). The purpose of this initial step is to learn, not to predict values of the target variable \(y\). The values of \(y\) are already present in the data table.
Training data: Data from which the machine learns the relationships among all the variables in the model to construct a prediction equation.
To continue the trendy anthropomorphic wording the machine learns enough to understand whatever relationship exists between target \(y\) and features \(X\).
The obtained prediction will not be perfect, but hopefully good enough to be useful. The goal is not to achieve perfect predictive accuracy, but instead better decision-making than not having the prediction.
1.5 Learn
The machine learns the patterns that relate the features to the target, expressed as a model. We inform the machine of only the general form of the model before learning begins, such as a weighted sum in our online clothing retailer example. From this general form, the machine analyzes the available training data to construct a specific model by estimating values of the weights. These weights optimize some aspect of predictive accuracy as it applies to the training data from which the model was derived.
We do not directly teach the machine.
The (estimation algorithm implemented on the) machine learns not by instruction but by example.
The machine learning software provides the instructions for the machine to learn by analyzing the examples.
For each row of the training data, the learning algorithm relates the values of the features to the value of the corresponding target. The value of the target variable for any row of data is the correct answer, the corresponding value of variable \(y\). This target variable provides the “supervision” that guides pattern discovery for the data related to it. Machine learning algorithms choose weights for the features so that, averaged across all the examples, the values of \(y\) computed from the model are as close to the actual values of \(y\) as possible.
Fitted value: Estimated value of \(y\) computed from the prediction equation, the model.
For each example, comparing this fitted value to the corresponding actual value becomes the basis for the machine learning the relationships.
Error: Difference between the actual value of \(y\), and the value of \(y\) fitted by the model.
The fitted value from the training data is not a prediction. The learning algorithm must know the correct answer for each of many examples. On the contrary, prediction applies to unknown values.
The machine generally discovers relationships by trial and error, applying a process called gradient descent. The algorithm examines each row of data, each example, to relate the \(X\) variables to \(y\). The algorithm, based upon the form of the analyst’s model, then tries various specific values for the weights across a series of successive steps. It revises the weights at each step, always obtaining less overall error averaged over all the examples at each successive step. At some point, the machine concludes it cannot find a set of weights that result in a meaningful amount of less error than already obtained, such as the weights 3.80, 7.32, and -386.22 obtained in our clothing example.
There are many possibilities for the machine to learn from the data. Choose from many different:
- Types of models such as linear regression and non-linear regression, support vector machines, random forests, and neural networks.
- Solution algorithms to estimate the weights of the given model.
- Specific settings chosen for the solution algorithm, each of which can be tuned to potentially obtain better predictive performance.
To learn how to do machine learning is to learn how to invoke these different types of models, estimation algorithms, and their associated settings to derive the most effective predictive model from a given set of data. An expert in machine learning understands all of these models and corresponding algorithms, how to implement them for computer analysis, how to best tune each procedure to obtain the best performance, and then ultimately deploy the learned model to the relevant prediction setting. To attain a high level of expertise requires much practice and some mathematical training to understand better how the different procedures work for more effective tuning.
Perhaps other algorithms or functional forms or features would have lead to a more useful predictive model in our online retail clothing example. Under the imposed functional form of a weighted sum, however, and given the chosen estimation algorithm, the resulting estimated weights – 3.80, 7.32, and -386.22 – minimize some function of the errors as applied to the training data.
1.6 Test
Teachers test students on their learning. The analyst tests the machine on its learning. People, and now machines, can try to learn, but was the learning successful? Maybe the person or machine could not apply a successful learning strategy, or maybe there was nothing there to learn, randomness rather than structure.
To validate an obtained model, test what the machine has learned on new examples, on previously unseen data. What is the source of this unseen data?
Testing data: A split of the original data held back from model estimation to test how well the machine can predict from new data.
Hopefully, in the era of big data, you have enough rows of data, examples, to split into two different sets, each large enough to fulfill their respective roles, training followed by testing.
The machine already knows the values of \(y\) for the training data, but not the testing data. The analyst, however, knows the values of \(y\) for each set of example values of X in both the training and the testing data.
Prediction: The fitted value the model computed from the values of the features from data on which the model did not train.
Splitting the original data into training and testing data sets is one of the most fundamental concepts of data science. Because the machine is unaware of the values of \(y\) in the testing data, the analyst can evaluate true forecasting efficiency of the model, that is, when \(y\) is unknown. When the model is applied to generate real-world predictions, neither the machine nor the analyst knows the value of \(y\).
As with the training data, define an error as the difference between the actual value of \(y\), and the model’s fitted value, the comparison of what is with what the model specifies to be.
Figure 1.4 illustrates a prediction, with an unknown value of the target variable.
The need to evaluate the model with new data reveals an essential, but sobering, reality of machine learning. The error of prediction from new data averages higher than the error from the model applied to the data from which the model was estimated.
The learning (estimation) process is biased in favor of the data on which it trained. The issue is that random variations across samples, sampling error, ensures that every sample is different, so applying the model to new data introduces new random fluctuations of the data.
Overfitting: The prediction model fits the training data too well, reflecting random perturbations of the training data sample that do not generalize to new samples.
An overfit model can compute values of the target that nicely match the true values of the already known training data and then fail miserably when predicting new data.
The goal of predictive (supervised) machine learning is not to develop a model that minimizes the errors on the training data, but instead minimizes the errors on the testing data.
In pursuit of a continually better fit, the analyst may adjust and re-adjust the learning process and the model itself, running and revising the learning procedure over and over on the same training data. To assess predictive accuracy by applying the model to the testing data is freedom. The analyst may freely tune the learning process with repeated modifications on the training data with one strong caveat: Test the final model on new data. A model cannot be properly evaluated on data for which it has been trained.
1.7 Explain
The complexity of some machine learning algorithms renders their inner workings uninterpretable. A machine learning analysis can focus primarily on predictive accuracy, with not much understanding of how values of the feature variables relate to a predicted value. With an emphasis on predictive accuracy, the specifics of how the values of feature variables lead to effective prediction may not be of much interest.
Black box prediction: A prediction model that provides no information as to how the values of each feature relates to the target.
This lack of understanding may follow from a simple lack of interest, or from the overwhelming complexity of the prediction equations. Simpler models, such as models expressed as a weighted sum of the variables, tend to be more interpretable.
For some forms of machine learning, the process of transforming the values of the predictor variables into a prediction is far too complex to render as a single equation. For example, a neural network may require the estimation of not two weights, such as in the previous example of the online clothing retailer, not even a hundred weights, but tens of thousands of weights distributed over multiple equations layered together to form an interconnected sequence, a network.
If the goal of the analysis is solely effective prediction, and if this effectiveness can be obtained without understanding the processes inside the black box, there may be no need for further understanding. Many scenarios, however, benefit from an explanation. Management and customers may want to know how the predictions are obtained. Regulators may demand such an explanation.
Explain: Understand how changes in the X variables relate to corresponding changes in the \(y\) variable.
The explanatory aspect of modeling attempts to answer the Why questions. Why did consumer demand drop for that product? Why did shipping costs rise? What attributes of a product enhance consumer satisfaction?
Prediction and explanation, moreover, are not mutually incompatible. Understanding the relation of the variables beyond prediction efficiency is relevant in many, if not most, applications. Even if the emphasis is predictive efficiency, understanding each feature’s impact on the value of the target can result in choosing features that more strongly influence the target variable, leading to more accurate prediction.
For example, how much does weight increase, on average, for each additional inch of height and chest size? For each year that a person works at a company, how much, on average, does salary increase? How much do home sales decrease, on average, for each rise of one percentage point in the interest rate? More generally, which features (predictor variables) have the most impact on the target variable?
Construct machine learning models to accomplish some combination of two goals:
1. Predict the value of a variable from other variables.
2. Understand/explain the relationship among variables.
When beginning a machine learning analysis, consider the purpose of the study. Is the emphasis on prediction or explanation and understanding of variable relationships? Often knowledge regarding both considerations is desired, but in some situations, construct the model to favor either prediction or explanation.
To maximize understanding of the relationships, enter a smaller number of more meaningful variables into the analysis. Much of modern machine learning focuses on predictive accuracy, with some models in some contexts built with hundreds of features. Still, the need for explanation and understanding remains in many contexts.
1.8 Procedure
Model construction follows a general procedure. Regardless of the specific model and the particular implementation of a learning algorithm, the overall predictive process remains the same.
- Prepare: Gather, clean, transform data as needed into a rectangular table, then split the data.
- Learn: Train the model on some of the data by minimizing a function of the discrepancy between the actual value of \(y\) with the value computed by the model.
- Validate: With the remaining data, calculate the predicted values, then match to the true values.
- Deploy: If validated with sufficient accuracy, apply the model to real-world prediction.
The magic of modern computing power and methods make the many already developed free machine learning tools accessible to all with a personal computer or access to cloud computing. Not too many years ago, someone doing machine learning needed the theoretical, mathematical tools to develop and implement the algorithms. That analyst required a massive budget for computer access. Today, those algorithms are neatly and efficiently packaged in user-accessible, free software modules, ready to use, such as with frameworks that run with the Python or R open-source computer languages on your computer.
Moreover, although some machine learning methods are elaborately computer intensive, the simplest estimation algorithms may work reasonably well, if not as well. Machine learning implementations usually present appropriate default settings for a particular estimation algorithm. The coding skill to implement machine learning, while not trivial, is also not substantial. Of course, a model built by a beginner may not attain the same predictive efficiency as a model built from the same data by an expert. Still, for a given scenario with modern, free computing tools, some basic analysis can result in a model that more effectively predicts with your model than without it.
Beyond these technical considerations, we have the reason for our interest in the analysis. Before beginning to analyze data, first, you need data. Data for what? The foundation of applying machine learning to solve a business problem is the precise understanding of that problem’s statement and scope, such as predicting future events. At the core of a successful machine learning analysis are the management insights gained from understanding how a specific predictive model creates value for your organization.