10.1 Overview
Supervised machine learning trains a prediction model from examples, individual rows of training data that include the values of the predictor variables and the target, the response variable. The model expresses a mathematical relationship between a set of predictor variables (features), X, with a target variable, \(y\). Predict the value of a target variable according to one of two types: continuous, with values on a numerical scale, and categorical, with a set of pre-defined categories or groups.
The topic here is the classification of an object of interest into a group or category, one group for each value of the categorical variable. We consider the primary situation, binary target variables, two levels only.
Consider examples of categorical target variables:
- shipment: late or on time
- loan: repay or default
- email: ham (legitimate) or spam
- customer: stay with subscription plan or churn (leave)
- customer: online purchase or leave web site
- applicant: hire or not hire
- student: pass or fail
- machined part: accept or reject
Each of these target variables represents a specific application. There are many more.
What can management learn about the likelihood that a shipment will arrive late? To label a categorical target value, such as a shipment’s on-time status, proceed as usual for a regression analysis: Collect information about the relevant characteristics, the predictor variables or features, plus the one response variable. In this example, the features describe various shipment conditions. Include variables such as the company of origin, the time of week, the time of day, the shipping company, and the priority level when developing a model to label a late shipment. Input the values of the predictor variables into the model to label the shipment’s status based on the estimated probabilities of each scenario.
However, a target variable composed of categories requires special considerations in terms of how to conceptualize, estimate, and assess model fit. Begin by assigning a generic name to one of the binary category target variable’s two values.
Reference group: Group on which the analysis is focused, scored a 1 in the analysis.
The late shipment group is the reference group if the goal is to understand why some shipments are late. If both groups are equally relevant from a business standpoint, such as man or woman body type sizing of clothing, choose one of the groups at random as the reference group. Or, if the choice is arbitrary, perhaps choose the reference group that leads to positive differences on all or most of the predictor variables to ease interpretation.
The model labels (predicts, classifies) group membership in terms of the estimated probability of membership in each group.
A predictive model for a target defined by distinct groups (categories) estimates the probability that a given observation (example, sample, instance) is a member of each group, from which to predict group membership.
Given information about the shipment from the values of the predictor variables (features), what is the probability \(p\) that a shipment will be late? Call the probability of membership in the reference group, such as a late shipment, as \(p\). For a target variable with two categories, the probability of membership in the other group, an on-time shipment in this example, is \(1-p\).
Given the probabilities of reference group membership, the model by default labels each instance (example, sample) for the group with the largest probability of group membership. With only two categories of the target variable, only two values are predicted. By default, score reference group membership as a 1. To classify an example into the reference group is to set \(\hat y = 1\). If the model classifies the instance into the remaining group, \(\hat y = 0\).
To predict the on-time status of a shipment, apply the model according to the conditions of the order fulfillment, the values of the predictor variables. These conditions become the values of the predictor variables for a specific instance, a specific shipment. Label shipments as late if the model returns a probability larger than the chosen threshold of being late, typically 0.5 for target variable with two categories. Choose the threshold based on the analysis of fit indices, as explained later.
The classification of the example, such as a shipment, answers the prediction question with probability that is used to classify an example as yes (1) or no (0). Will the shipment arrive on time? Will the applicant be hired? Will the customer default on the loan? Will the customer respond to an email advertisement? Predictive models of a target with two values ultimately resolve to a yes (1) or no (0) label with a corresponding estimated probability of membership in each group.
10.2 Binary Classification
Many machine learning methods can predict a categorical target variable from a variety of models based on the estimated probabilities of an outcome. Logistic regression of a linear model is the classic and historically prior example and is the method discussed later. Regardless of the specific form of the model and the specific solution (learning) algorithm, all such classification procedures share a set of common concepts with a shared common language.
10.2.1 The Classification
Binary prediction applies when the target variable, the variable to be predicted, has only two unique values.
Binary variable: A variable with only two unique values.
Labeling an example according to its predicted group membership is classification. The classification labels an example (represented by a row of data), with one of the target group names.
Label: The name of a specific group for a categorical the target (response) variable.
The output of the model of a categorical target value is a label, a group or category name.
Classification: Assign group membership to the example (sample, instance) by assigning a label, the name of a group.
The variable, shipment arrival times, for example, defines two groups. Shipments either arrive on time or they are late. A successful machine learning prediction model correctly labels the shipment before it is received and then reveals why a shipment did or did not arrive on time.
Multiple benefits accrue from successful prediction. The prediction alerts the receiving company to the possibility of a late shipment, providing management with the information necessary to correct the issue before it occurs. Management may then be able to take preventative measures in advance. Ship at a different time of day or increase the priority level, for example. A successful prediction model also notifies the shipping company of the reasons for the shipment’s late arrival. The shipping process can then be re-engineered to produce fewer late shipments in the future.
Different sets of general, generic labels describe the two groups: positive-negative, yes-no, and true-false. The generic labels most often employed are positive-negative, where positive indicates membership in the reference group (scored 1), and negative means not a member (scored 0).
Positive outcome: Membership in the reference group.
Somewhat confusingly, “positive” does not imply a favorable or desired outcome. With the focus on late shipments, define that group as the reference group. A late shipment is a “positive” outcome from the perspective of prediction, but of course, a failure from the business perspective. More dramatically, a “positive” result in medical research may indicate that the patient has cancer.
10.2.2 Classification Outcomes
10.2.2.1 The Concept
The essential characteristic of binary classification is that labeling membership into one of two groups generates four outcome possibilities.
A binary prediction provides two ways to be right and two ways to be wrong.
Figure 10.1 illustrates the four possible outcomes for a binary prediction.
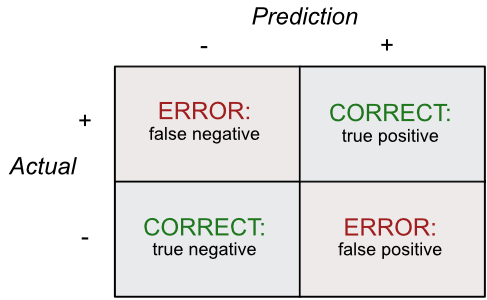
The two ways to predict the correct label:
- True positive: Correctly labeled as member of the reference group.
- True negative: Correctly labeled as not a member of the reference group.
The two ways to predict the wrong label:
- False positive: Mistakenly labeled a member of the reference group.
- False negative: Mistakenly labeled as not a member of the reference group.
Read “false positive” as falsely labeling an instance as positive. Similarly, “false negative” means falsely labeling an instance as negative.
These four outcomes describe what the model correctly labels (predicts) and what it incorrectly labels. As with any prediction, evaluate prediction effectiveness by comparing some function of what is correct, \(y_i\), with what the model claims is true, \(\hat y_i\). From the four possible outcomes of a binary prediction, obtain the residuals across all \(n\) rows of the data (the three-pronged equals sign, \(\equiv\), means true by definition):
\[e_i \equiv y_i - \hat y_i\] The concept of a residual from a binary classification analysis reduces to the 2x2 table in Figure 10.1 that tallies the counts for each of the four cells.
Confusion matrix: Table that lists the numbers of the four outcomes of a binary prediction classification.
The residual for a correctly labeled example is a perfect 0. If not correct, when the reference group membership is scored a 1 and not in the reference group is scored a 0, the residual is \(+1\) or \(-1\). A false positive predicts a 1, but the value is 0, so the residual is a \(0-1=-1\). Similarly, a false negative generates a residual of \(+1\).
10.2.2.2 Example
This section continues the online clothing retailer example from the linear regression chapter, with the version of the data set with 340 rows of data. The data are evenly split between men and women body types, coded as M and W. Here, Gender is the missing data value for a customer order. The retailer wishes to label the value from the other provided physical dimensions. Begin with a single predictor variable of Gender, the value of Hand size, measured in inches.
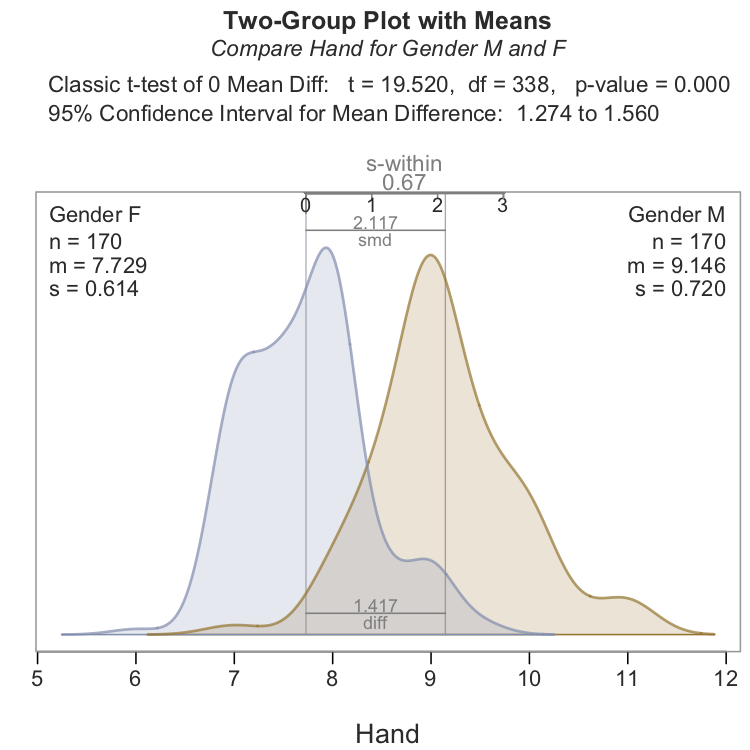
Hand size may be a relevant predictor of Gender given the difference in mean hand width for these data, 9.15 inches for men/8.40 and 7.73 inches for women. To explore relevance, the relation between the predictor and the target, evaluate the mean difference of Hand size for men and women, which is 1.42 inches for this particular data set, illustrated in Figure 10.2.
The corresponding \(t\)-test of the mean difference is significant, with \(p\)-value \(=0.000\), zero to three decimal digits. If the null hypothesis of no difference of Hand size across the two genders is true, a very unlikely event occurred with a sample mean difference as large as 1.42 inches. The resulting sample distributions follow, which illustrate the different average Hand sizes for these two genders and their corresponding distributions. 1
1 t-test visualization from my R package lessR tt_brief(Hand ~ Gender)
Given the large difference in mean Hand size across men and women, Hand size appears to be a relevant predictor variable or feature for Gender classification. From the estimated model, compute the probability of being a man or woman from a given Hand size. Arbitrarily select man as the reference group, so score male membership as a 1, if for no other reason that a positive difference in Hand size is perhaps a little easier to interpret. Label samples with a probability of a man greater than or equal to 0.5. A probability less than 0.5 results in a label of woman.
Analyze the single predictor model of Gender from Hand size with logistic regression, one of many possibilities for machine learning algorithms. With this simple model, anyone with a Hand size larger than 8.4 is labeled as Man. A Hand size less than 8.4 results in a label of Woman.
From this decision criterion, and knowledge of the correct label, the value of y, focus on the resulting confusion matrix that resulted from applying the model to the rows of training data. How many predicted values occur in each of the four cells in Figure 10.1? The confusion matrix from predicting Gender from Hand size follows.2
2 Confusion matrix from my R package lessR Logit(Hand ~ Gender) function
Probability threshold for predicting M: 0.5
Corresponding cutoff threshold for Hand: 8.408
Baseline Predicted
---------------------------------------------------
Total %Tot 0 1 %Correct
---------------------------------------------------
1 170 50.0 17 153 90.0
Gender 0 170 50.0 147 23 86.5
---------------------------------------------------
Total 340 88.2Next, interpret the numbers in the confusion matrix.
10.3 Classification Fit Metrics
Classify an example according to the probability of membership in each group calculated by the model. To evaluate model fit, for each example in the data table compare the actual label to the predicted label. A variety of metrics for evaluating classification fit follow from that comparison. Each fit metric results from the counts in the four cells identified in the confusion matrix found in Figure 10.1. Different fit metrics provide different information. Which fit metric provides the most useful information depends on the specifics of a given prediction situation.
10.3.1 Baseline Classification
Included in this confusion matrix is the table heading Baseline.
Baseline probability: Probability of membership in each group based on the total number of examples (rows of data) in each group.
The baseline probabilities provide the anchor, the null model, computed without reference to the one or more features of the model.
Null model classification prediction: Label each instance according to the group with the largest membership.
Instead of using values of X to predict \(y\), the null model uses only information regarding the target, \(y\). Given no other information, the largest number of correct predictions results from labeling membership into the most frequently occurring group. In these data, man (1) and woman (0) are evenly split, so the baseline probability is 50%.
Analogy of \(R^2\) for predicting a binary target: How much improvement in classification results from using the feature to predict the target beyond the baseline probability?
Compare the largest baseline probability to the classification probability of the model with the features. For this example, how much better is classification using the model over the baseline probability of 50%?
10.3.2 Accuracy
The most basic information gleaned from the confusion matrix is the proportion of correct classifications. What proportion of examples (row of data) were correctly labeled as either in the reference group or in the other group, positive or negative?
Accuracy: Proportion of correctly labeled examples.
\[ \mathrm{accuracy = \frac{true \; positives + true \; negatives}{all \; outcomes}}\]
The accuracy fit index is the proportion of correct classifications.
Compute the overall accuracy directly from the preceding confusion matrix.
\[ \mathrm{accuracy = \frac{true \; positives + true \; negatives}{all \; outcomes}} = \frac{147 + 153}{147 + 23 + 17 + 153} = 88.24\]
In this example, accuracy is 88.2%, with 17 false negatives, men mislabeled as women, and 23 false positives, women mislabeled as men.
Need to improve accuracy? Then build a better model. Just as with least-squares regression to predict the value of a continuous variable, one strategy adds relevant predictor variables to the model that each provide relatively unique information regarding the target variable.
10.3.3 Alternatives to Accuracy
With any classification model the ideal outcome is perfect classification: In the reference group (\(y=1\)) or out (\(y=0\)). Unfortunately, only trivial models achieve perfect classification. Mis-classification results from some combination of false negatives and false positives. However, in many situations the outcome of one type of mis-classification has more severe consequences than the other type. Accuracy is not the most useful fit index when the costs of the two types of errors differ, especially when they dramatically differ.
Consider an aircraft manufacturer that receives a machined part from a supplier. Suppose that 99.9% of these delivered parts are within specs and properly manufactured. Predicting all parts to be quality parts provides a prediction accuracy of 99.9%. The classification procedure in this scenario only mislabels 0.1% of the delivered parts!
Extremely high accuracy in classifying the manufactured parts, yet a potential colossal failure. Failure of the aircraft part is potentially catastrophic. All the mis-classified parts are failed parts. Extremely high accuracy results in an unacceptable outcome: One out of a thousand aircraft with the installed part eventually crashes.
Differential, asymmetric consequences of the two types of mis-classification imply that the chosen fit index should differentially weight the two types of mis-classification.
Select the appropriate asymmetric classification fit index, once more derived from the confusion matrix, to more severely penalize the more severe error when one type of error is more consequential than the other.
The issue is the inherent tension between the two types of mis-classifications: false positives and false negatives.
For the same data, decreasing false positives leads to an increase in false negatives, and vice versa.
For a given data set, both errors cannot be simultaneously decreased. To adjust the model to decrease one type of error also increases the other type of error. The only way to simultaneously reduce both types of errors is to build a new, better model.
To focus on either the number of false positives or false negatives for the current model, consider two ratios developed for that purpose. One fit index, sensitivity (recall) becomes smaller as the number of false negatives become smaller. Another additional fit index, precision, becomes smaller as the number of false positives becomes smaller. Both of these fit indices complement accuracy, appropriate when the costs of both types of mis-classifications are equal.
10.3.4 Sensitivity
To continue the aircraft part scenario, provide data that results in a decision criterion that identifies all failed parts, those parts destined to fail prematurely when placed in operation. An appropriate fit index must directly reflect the false negatives that result from the classification procedure, and only equal a perfect score of 0 when the number of false negatives is zero.
The reference group in this example consists of the parts that fail, the positive outcome for purposes of analysis. The negative group consists of the good parts. The airline manufacturer must completely avoid a part that is falsely classified as good (labeled negative group outcome) even though it will eventually fail (actual positive group outcome). Identify all parts that would eventually fail, the false negatives, parts labeled to be good (negative outcome), but destined to fail (positive outcome).
Preliminary testing gathers various measurements of each delivered part. Enter the gathered information into the model, calculate the prediction, and then correctly label all parts destined to fail. Neither error is desired, but altogether avoid a strategy that can yield a false negative, a strategy that necessarily increases false positives. A false positive is expensive, requiring additional testing, but not catastrophically expensive.
In this situation, the overall accuracy of classification is irrelevant. Instead, consider another fit metric.
Sensitivity (or Recall or True Positive Rate): Proportion of actual positive instances correctly detected as positive.
If the instance (sample) is positive, sensitivity is the probability of correctly predicting positive. In this example, sensitivity indicates the proportion of bad parts that get identified as bad. Sensitivity in this situation of the aircraft part needs to be 100%.
Sensitivity indicates the proportion of actual positive occurrences (here referring to failure) correctly labeled to be positive (to fail). What is the sensitivity of the model to detect, to recognize positive group membership (here failure) when it occurs? Was the part destined to fail identified as such by the model? The positive examples include all of those correctly labeled as positive, the true positives, and those in the reference group but falsely labeled as not in the group, the false negatives.
\[ \mathrm{sensitivity = \frac{true \; positives}{true \; positives + \color{RoyalBlue}{false \; negatives}} = \frac{true \; positives}{\mathit{actual} \; positives}}\]
With the number of false negatives in the denominator, sensitivity increases as the number of false negatives decreases. Sensitivity is a perfect 1.0 or 100% only when there are no false negatives, every positive instance is correctly classified.
Applied to the previous example:
\[ \mathrm{sensitivity = \frac{true \; positives}{true \; positives + false \; negatives}} = \frac{153}{153 + 17} = 90.00\]
Higher sensitivity implies lower false negatives.
Regarding the aircraft parts, the explicit goal is \(\mathrm{sensitivity}=1\), no false negatives. Identify all parts in the fail group. The consequences of a false negative demand that the preliminary test of quality provides perfect sensitivity.
Because the information from the features to label group membership is not perfect, one possibility generates new data by increasing the rigor of the quality test. This more rigorous test is more expensive to implement, but leads to a decrease of false negatives, parts doomed to fail that are disastrously labeled into the quality group (negative outcome). The opposite, making the test less rigorous, allows more disastrous false negatives of the aircraft parts.
10.3.5 Precision
In the analysis of aircraft parts, sensitivity is the most important factor for identifying parts that will eventually fail. False negatives are unacceptable. Neither misclassification error is desired, however. In this aircraft part scenario, minimizing false positives is a secondary goal. Each false positive from the initial test, a good part misidentified as a bad one, necessitates costly additional testing. This additional testing is significantly more costly than the preliminary test, but not nearly as costly as the operation of a defective part. Nonetheless, a misclassification error is still an error, and errors are costly.
In this analysis, the reference group is comprised of failed parts, so a positive result indicates a failed part. The total number of labeled (predicted) failed parts is the sum of the number of true positives, or those correctly labeled to fail, and the number of false positives, or those incorrectly labeled to fail. Precision is the proportion of correctly labeled positive outcomes to the total number of labeled positive outcomes.
Precision (or positive predicted value): Proportion of correctly labeled positive outcomes.
If the prediction is positive, precision is the probability the sample is actually positive. How precise is the prediction for correctly labeling positive outcomes?
\[ \mathrm{precision = \frac{true \; positives}{true \; positives + \color{RoyalBlue}{false \; positives}} = \frac{true \; positives}{\mathit{labeled} \; positives}}\]
With the number of false positives in the denominator, precision increases when the number of false positives decreases, when labeled as reference group members are reference group members. Precision can be a perfect 1 or 100% only when there are no false positives, when every instance of a negative outcome is correctly identified.
Higher precision implies lower false positives.
Precision indicates the model’s ability to avoid labeling as positive group membership when that instance is actually negative.
Applied to the previous example:
\[ \mathrm{precision = \frac{true \; positives}{true \; positives + false \; positives}} = \frac{153}{153 + 23} = 86.93\]
In this example, Precision of 86.9 is less than Sensitivity (Recall) of 90.0 because there are more false positives, 23, than false negatives, 17.
10.3.6 Sensitivity with Precision
As precision increases, sensitivity (recall) decreases, and vice versa. Ideally, both recall and precision would achieve their maximum value of 1. However, the ideal does not happen with non-trivial classification given underlying uncertainty. Instead, identify the costs of mis-classification for a false negative or a false positive, then proceed accordingly to adjust the model to favor recall, favor precision, or favor some combination of both.
Sensitivity and precision are each typically less than 1, but greater than their minimum values of 0. The goal for many classification models balances both indices. To equally balance both fit metrics, take the mean. In practice, the mean of the fit indices is not the standard arithmetic mean, but rather the average implemented as the harmonic mean. The arithmetic mean divides the sum of the values by the number of values. The harmonic mean sums the reciprocal of the values.
Harmonic mean: Sum of the reciprocals of the set of values, divided by the number of values.
The desirable property of the harmonic mean is relative insensitivity to outliers compared to the arithmetic mean.
Applying the harmonic mean to sensitivity and precision leads to the following definition of another fit metric. The harmonic mean is the reciprocal of the arithmetic mean of the reciprocals.
\[F_1 = \frac{1}{1/2 \left(\frac{1}{\mathrm{sensitivity}}\right) + 1/2 \left(\frac{1}{\mathrm{precision}}\right)}\]
Typically write the harmonic mean of sensitivity and precision as the following with the application of a little algebra to the above defining formula.
\[F_1 = 2 * \frac{\mathrm{sensitivity * precision}}{\mathrm{sensitivity + precision}}\]
If both sensitivity and precision are low, \(F_1\) cannot be large because it averages the two mis-classification indices.
Other such \(F\) statistics are available that apply more weight to sensitivity or to precision, leading to an entire family of such statistics. The \(F_1\) statistic, however, is the most commonly applied version.
10.3.7 The Probability Threshold
The previous example used the default probability cut off 0.5. For example, changing the threshold to 0.4 for predicting a man from Hand size increases the number of predictions for a man from the same data set.3 Some of these instances now predicted to be a man will, in actuality, be a woman, so the number of false positives will increase.
3 If using R with my lessR ;package, change this threshold for the lessR function Logit() with the parameter prob_cut.
4 Obtained from the lessR function Logit(): Logit(Gender ~ Hand, prob_cut=0.2).
To illustrate, decrease the probability threshold from its default value of 0.5 to 0.2. The following table shows the resulting confusion matrix.4
Probability threshold for predicting M: 0.2
Corresponding cutoff threshold for Hand: 7.975
Baseline Predicted
---------------------------------------------------
Total %Tot 0 1 %Correct
---------------------------------------------------
1 170 50.0 2 168 98.8
Gender 0 170 50.0 87 83 51.2
---------------------------------------------------
Total 340 75.0Lowering the probability threshold from 0.5 to 0.2 lowers the corresponding threshold for Hand size from 8.408 to 7.975 inches. The result is a drastic increase in the number of False +’s, from 23 to 83. However, the number of False -’s, dramatically decreases from 17 to 2. As such, avoiding so many more False -’s increases sensitivity from 92.35 to 98.82, but the increase in False +’s decreases precision from 87.22 to 66.93.
10.4 Logistic Regression
Is the shipment predicted to arrive on time or be late? We need a model from which to calculate the corresponding probability of a binary outcome from the values of the predictor variables. If the probability is higher that the shipment will be late than on time, then our prediction (classification, labeling) is a late shipment. With that knowledge, we either accept the likely delay of the shipment, or change the shipping conditions to facilitate an on-time delivery.
How can a model be constructed and estimated to calculate the probabilities of classifying instances such as these? Various models, including linear models, are available for predicting (classifying, labeling) the value of a categorical variable. As with predicting the value of a continuous variable, there are also a variety of estimation algorithms for classification models, depending on the model’s structure. Logistic regression, which was developed in the 1930s, is the most well-established estimation method for classification from a linear model.
10.4.1 Traditional Regression Not Suitable
The software for logistic regression assumes that the values of the target variable are encoded as 0 for non-members and 1 for members of the reference group. Although limited to only two numeric values, the values are numeric, so conventional least-squares regression analysis can be applied to these data. A least-squares regression analysis computer program can perform the analysis and generate output for predicting a binary target variable scored as 0s and 1s. The issue is that the analysis lacks meaning.
To illustrate, let’s continue with the example of using Hand size to Predict Gender, where Male is an arbitrary reference group scored a 1. Figure 10.3’s scatterplot illustrates one reason why the prediction of a binary target variable is inappropriate.
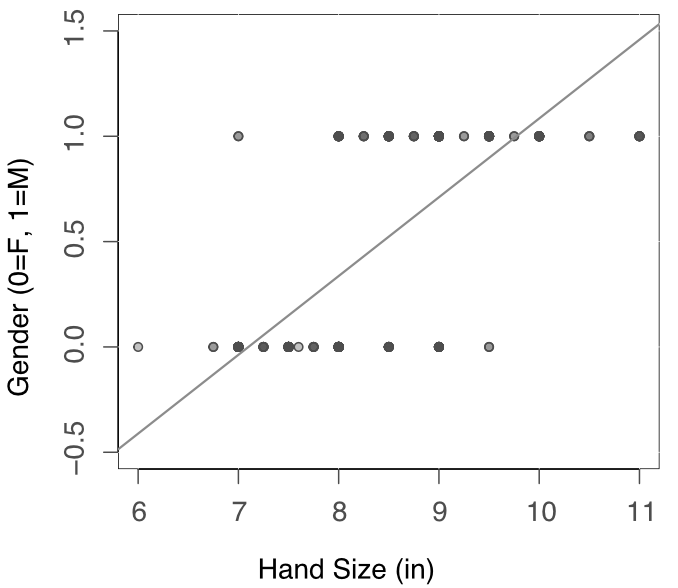
The response variable Gender has only two values, 0 and 1, yet the fitted values from the resulting estimated regression line are continuous and assume values that are not interpretable. Instead of a label, the output is numeric. The corresponding fitted value for Hand size of 9 inches from the regression line in Figure 10.3 is \(\hat y_{Gender}=0.711\). What does a Gender of 0.711 mean? Or, how about an out of range fitted value that results from a Hand size of 6, which yields \(\hat y_{Gender} = -0.411\)?
Moreover, the least-squares estimation procedure applied to a binary response variable necessarily violates some assumptions. One issue is that the residuals cannot be normally distributed because each residual is calculated with a subtraction of a value from only 0 or 1. The residuals for a binary response are \(e_i = y_i - \hat y_i\), where \(y_i = 0\) or \(y_i =1\). Instead of a continuous distribution across the range of a normal distribution, the residuals cluster only around these two values.
10.4.2 Logistic Regression Model
The key to correctly modeling a binary response variable switches the focus from the values of the response variable to the probability of group membership for the reference group. For example, given a specific Hand circumference, what is the probability that the person is a man? Given the probability of being a man, the probability of being a woman is one minus that probability.
10.4.2.1 Logit as the Target Variable
To construct an expression that computes the probability of reference group membership, a “success”, statisticians discovered the key is to begin with the concept of the odds of an event, an alternative expression of probability.
Odds Ratio: Ratio of the probability of the event occurring to the probability of not occurring.
Expressed as an equation, define the odds ratio as:
\[odds = \frac{p}{1-p}\]
Note the distinction between probability and odds. The probability of rolling a 3 for a six-sided die (singular for dice) is 1/6. The probability of not rolling a 3 is 5/6. Express the odds of rolling a 3 as the ratio:
\[odds = \frac{p}{1-p} = \frac{1/6}{5/6}=\frac{1}{5}=0.20\]
The odds ratio, or refer to as odd, is the number of ways to get the designated outcome to the number of ways to not get that output. In this example, there is 1 way to get a 3, and 5 ways to not get a 3.
The next step the statisticians discovered for getting the calculated probability is to take the logarithm of the odds ratio, which defines the target or response variable over all possible values. Odds can only be positive numbers. In contrast, the logarithm of the odds varies from negative to positive infinity. The odds of an event with a probability of 0.5 are 1. The corresponding natural logarithm of 1 is 0, the boundary between an event with either less or more than a 0.5 probability. A probability much smaller than 0.5, close to zero, yields a very large negative value. A probability closer to 1 yields a substantial positive value.
Logit: Logarithm of the odds ratio for the occurrence of an event, such as the membership in the reference group.
The logit of reference group membership becomes the target (response) variable of a linear model with weights estimated by logistic regression. The classification is binary, but the logit as target variable is continuous, spanning all numbers from indefinitely small to indefinitely large.
Logistic regression: The regression analysis of the logarithm of the odds ratio of a categorical target variable.
Regression analysis of a linear model requires, of course, a linear model. Express the logit transformation as a linear function of the predictor variables, where ln is the natural logarithm of the resulting expression. Define the probability \(p\) as the probability of an example being in the reference group for a given value of predictor variable \(x\).
The resulting logistic regression model defines the target variable \(y_{logit}\) as the logit estimated from the corresponding linear function of the predictor variables. That is, for the single predictor logistic regression model: \[\hat y_{logit} = ln\left(\frac{p}{1-p}\right) = b_0 + b_1 x\]
This is the model estimated by logistic regression analysis.
10.4.2.2 Estimation
The training data for a logistic regression contains for each example the values of the predictor variable and the corresponding actual classification, such as Hand size and Gender for each person. Unlike least-squares regression, the actual value of the target variable for each example of the training data, the logit, is not available for the estimation procedure. Because the value of \(p\) for the values of the predictor variables for a given row of data are not known at the time of estimation, the logit cannot be directly computed before the model is estimated. Without the value of the target variable, least-squares estimation is not available.
As with most machine learning algorithms, and unlike least-squares solutions, there is no analytic solution for the parameter estimates available by solving the equations needed to obtain the parameter estimates. Instead of minimizing squared errors, the usual estimation procedure for the logistic regression parameters is called maximum likelihood. The mathematical details of this solution method are not our focus beyond understanding that the coefficients of the model are estimated by the iterative method called gradient descent. The learning begins by calculating the likelihood for one set of initial estimates, more or less arbitrarily chosen. The estimation algorithm iteration-by-iteration successively adjusts the estimates to produce a greater likelihood for each iteration of the gradient descent. The iterations stop when the algorithm converges to a solution.
Convergence: Successive iterations of a gradient descent solution algorithm yield model estimates that no longer change (below some small threshold) with continuing iterations.
Some attempted solutions never converge, so the estimation procedure programmed in software has a default value for the maximum number of iterations before stopping. When running an analysis, sometimes a warning is given that the maximum number of iterations has been reached without the solution converging. In that situation, unless the data set is very large, increase the default value of the corresponding parameter (max_iter in sklearn Python) to determine if convergence can be attained.
10.4.2.3 Probabilities from the Model
The target, response variable, of the logistic regression model is the logit, the natural logarithm of the odds ratio for the probability of membership in the reference group. That variable, however, does not provide the basis for classification. What is needed is the ability to compute from the values of the predictor variables, the features, the probability of membership in the reference group, such as the probability of being Male.
The ability to compute these probabilities is why the logit serves as the target variable for the logistic regression. The computation of this probability requires the value of the logit, \(\hat y\), from the logistic regression. From the expression for the logit, algebraically solve for \(p\), the probability of membership in the reference group for each value of \(x\).
The following general solution from the logit follows from the fact that the inverse of the natural logarithm is the exponential function, based on the constant value \(e\). The function is called a sigmoid function, which transforms any value, from very small to very large, into the range from 0 to 1.
\[p = \frac{1}{1 + e^{-(b_0+b_1x)}} = \frac{1}{1 + e^{-\hat y_{logit}}}\]
The result of the logistic regression is not the straight line of traditional regression analysis in Figure 10.3. Instead, the visualization of this equation is the S-shaped probability curve in Figure 10.4, called a sigmoid curve. This curve is an appropriate replacement for the linear function in Figure 10.3, resulting directly from the choice of the natural logarithm of the odds ratio for the target variable in logistic regression.
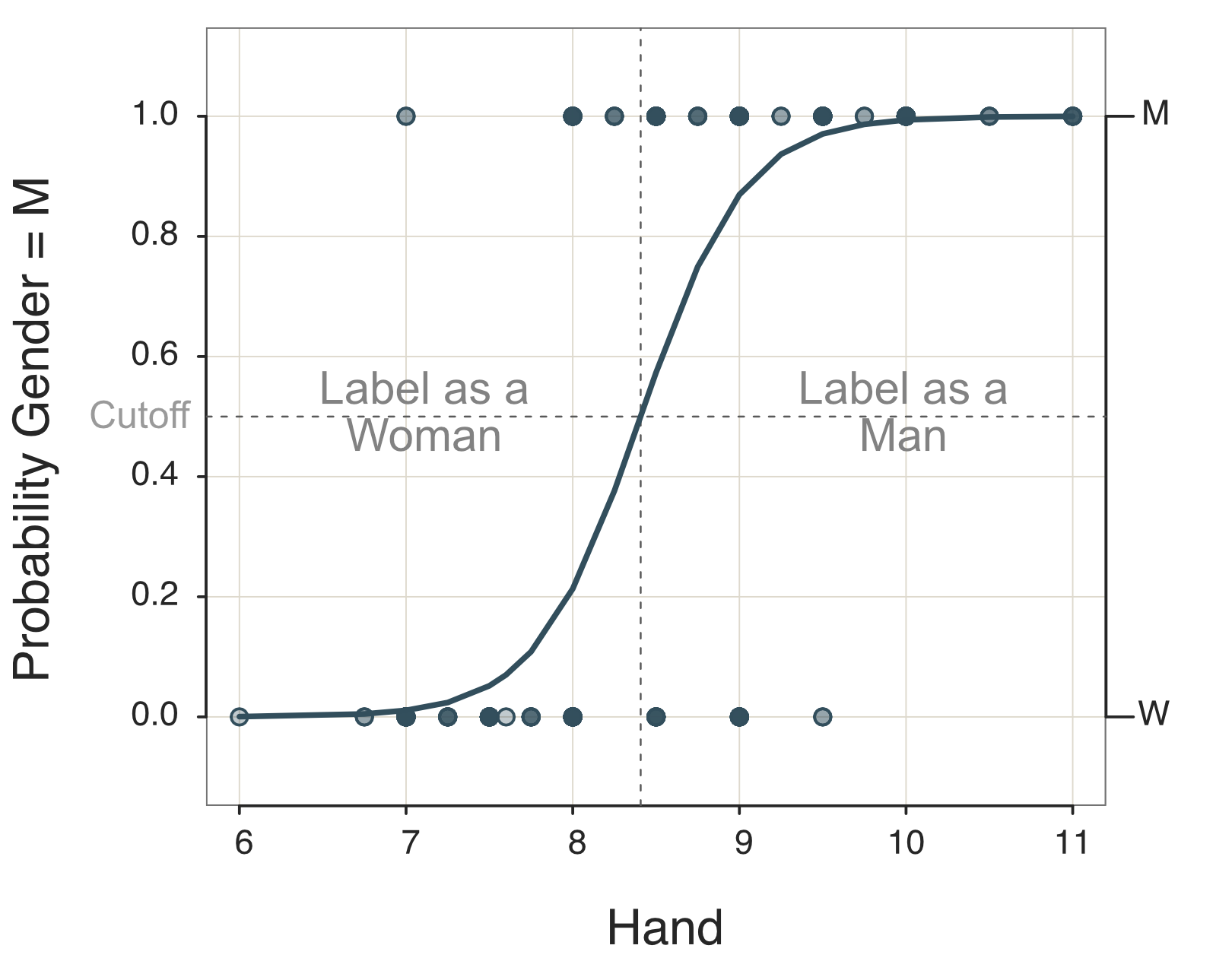
Figure 10.4 consists of two plots. The plotted sigmoid curve is the estimated probability distribution of Gender depending on Hand size, according to the left-vertical axis. Calculate this curve from the above sigmoid function given the parameter estimates \(b_0\) and \(b_1\).
The other plot is the scatterplot of the data, Gender with Hand size, specifically, M with Hand size and W with Hand size. The scatterplot is indicated by the right-vertical axis. The points in the scatterplot are plotted with transparency, so darker points represent more over-strikes than lighter points. The reason for the over-strikes is that Hand size is measured only to the nearest quarter-inch, so there are limited possibilities for the value of the x-variable, Hand size.
10.4.2.4 Classification from the Probabilities
The natural logarithm of the odds ratio is chosen as the target variable in logistic regression so as to obtain the corresponding solution for the sigmoid function for computing the probability of group membership. Then calculate \(p\), the probability an example is a member of the reference group given the value of \(x\), the predictor variable. Our focus is on the practical implication of applying these computed probabilities to classify.
Our primary goal is to correctly classify a given example (a row of data), the value of y, either a 0 or a 1.
From these probabilities in Figure 10.4, derive the decision rule for classification. On the left-vertical axis, choose a probability threshold for predicting M such as the default 0.5. Then, on the horizontal axis, choose the corresponding cutoff threshold for Hand that intersects the curve at the probability threshold, 8.408 in this example.
Decision Rule for Predicting Group Membership: Label all people with unknown Gender with Hand sizes above 8.408 as men and all people with Hand sizes less than that threshold as women.
From a practical perspective, to ask how well the model fits is to ask how well does the model correctly classify from given values of the predictor variables. The generally most useful fit indices of a classification model follow from the resulting confusion matrix: Accuracy, Sensitivity, and Precision. Choose the most useful fit index for a given situation. Perhaps vary the probability threshold for classification into one group or the other. Try various models (on training data) to choose the model that provides the best fit and then, as always, verify the model on testing data.
For logistic regression with multiple predictor variables, the sigmoid function and classification thresholds cannot easily be displayed, if at all. The same principles, however, apply. There is now a multiple dimensional sigmoid function, and a classification into the reference group is now based on the values of multiple predictor variables. The result continues to be a classification into the reference group given the corresponding probability of membership computed from the values of the predictor variables.
10.4.3 Interpret Slope Coefficients
The goals of regression analysis for logistic regression are the same as they are for least-squares regression: (a) Prediction and (b) understanding the impact of features on the target variable. Understand the relationship between the variables by interpreting the slope coefficients. The formulation of a logistic regression model as a linear regression model is critical for understanding the parameter estimates, the \(b's\).
10.4.3.1 Estimated Slope Coefficients
Consider the following output of the estimated logistic regression model for predicting Gender from Hand size.
Estimated Model for the Logit of Reference Group Membership
Estimate Std Err z-value p-value Lower 95% Upper 95%
(Intercept) -26.924 2.752 -9.785 0.000 -32.317 -21.531
Hand 3.202 0.327 9.794 0.000 2.562 3.843From the computer output we can write the estimated logistic equation.
\[y_{logit} = ln\left(\frac{p_{Male}}{1-p_{Male}}\right) = -26.9237 + 3.2023 X_{Hand}\]
The estimated logistic regression slope coefficient for Hand is 3.3023. Logistic regression models the logit, the logarithm of the odds ratio for reference group membership, here Male. For each additional inch of Hand size, the logit increases, on average, by 3.20. Unfortunately, knowing the impact of Hand size on the logit, the logarithm of the odds, is generally not a useful answer to understanding the relation of Hand size to Gender. We simply do not have an intuition as to the meaning of the change in the value of the logit.
10.4.3.2 Odds Ratio
A simple transformation yields a more useful interpretation of the slope coefficient, to indicate how the change in the value of \(x\) impacts the odds of being in the reference group, here Male. As stated, the exponential function applied to the logarithm returns to the original value. The exponential function applied to the logarithm of the odds on the left-side of the regression model returns the odds.
Applying exponentiation to the right-side of the logit regression model and working through the algebra results in the following statistic of interest: exponentiation applied to the estimated slope coefficient. For the Hand size relative to the logit:5 \[e^{3.2023} \approx 24.59\] This transformation of the slope coefficient from the logit regression model turns out to be the ratio of the odds for \(x+1\) to the odds for \(x\).
5 With R, exp(3.2023)=24.59. With Python, np.exp(3.2023)=24.59, where the numpy package is imported as np.
Odds ratio: For a one unit increase in \(x\), the ratio of the odds for \(x+1\) to the odds of \(x\), which is equal to \(exp(b_x)\) where \(b_x\) is the slope from the logistic regression.
The ratio of the two odds indicates the change in the odds of membership in the reference group for a one-unit increase in \(x\), consistent with the interpretation of a slope coefficient. The advantage of the odds ratio is that it is interpreted with respect to the odds instead of the logarithm of the odds from the original solution.
With the odds as the transformed target variable, the slope coefficients are interpreted in terms of their impact on the odds. How to interpret these odds ratios?
An odds ratio of 1.0 indicates no relationship between predictor and response variables.
No relationship between predictor variable and outcome of the target variable means that either outcome is equally likely from an increase of one unit in the value of \(x\). This value of 1.0 indicating no relationship is analogous to 0 indicating no relationship for the slope coefficient in the original model. This equivalence is also demonstrated by exponentiation of 0. \[e^0 = 1\]
Values of the odds over 1.0 indicate a positive relationship of the predictor to the probability that the value of the response variable is 1, a member of the reference group. For example, an odds ratio of 2 indicates a doubling of the odds of “success” for each unit increase in \(x\). For an odds below 1.0, the relationship is an inverse relationship. As the value of \(x\) increases, the probability of membership in the reference group decreases.
As always, generalize the sample results to the population.
A confidence interval of an odds ratio that spans values from below 1 to above 1 indicates that there is no relationship detected of the predictor variable to the classification of the target variable.
An odds ratio with all values above 1 throughout the range of the confidence interval indicates a positive (+) effect, an increase in the odds for a unit increase in \(x\). An odds ratio with all values below 1 throughout the range of the confidence interval indicates a negative or inverse (-) effect, a decrease in the odds of occurrence in the reference group for a unit increase in \(x\).
The estimated intercept and slope in relation to the odds and the corresponding 95% confidence interval for Hand size on classification as a man follow, from another part of the output of a logistic regression model.6
6 Output from my lessR Logit() function.
Odds Ratios and Confidence Intervals
Odds Ratio Lower 95% Upper 95%
(Intercept) 0.0000 0.0000 0.0000
Hand 24.5883 12.9547 46.6690The odds apply to membership in the reference group. The slope for the odds ratio of 24.59 is considerably larger than 1.0, so there is a positive relationship of Hand circumference to being a man in this data set, the reference group in this analysis. For this sample of 340 people, the odds that a person is a man are almost 25 times as likely, 24.59, for each additional inch of Hand circumference.
In the population, this odds ratio, with 95% confidence, is somewhere between 12.95 and 46.67. Interpreted, the true odds that a person is a man, for a one-inch increase in Hand size, increases somewhere in the range of about 13 to 46 2/3. Always interpret the results as they apply to the population, generalizing beyond the particular and arbitrary sample from which the model is estimated.
10.4.3.3 Impact of Scale
The odds ratio of 24.59 is so much larger than 1.0 because of the unit of measurement, inches, as a percentage of Hand size. Measuring Hand size in inches yields a range of sizes between 6 and 12. Each inch spans a considerable portion of the range from 6 to 12 inches. The result is a dramatic increase of the odds that a random selection of people from a sample all with the same increased Hand size yields a Male.
To illustrate, convert the Hand measurements from inches to centimeters by multiplying each Hand measurement by 2.54. Create a new variable in the d data frame, Hand.cm. Then re-run the analysis.
d$Hand.cm <- 2.540*d$Hand
Logit(Gender ~ Hand.cm)A centimeter is much smaller than an inch, so the resulting odds ratio decreases dramatically, from 24.59 to 3.53. The odds of selecting a man for each increase of one centimeter in Hand circumference increases, but not as much as for an increase of the much larger inch. There are different units for the two analyses, but invoking either unit indicates the same relationship.
10.4.4 Summary
The key to developing a regression model to predict group membership is to set the target variable as the logarithm of the odds of being in the reference group. With this target variable, algebraic transformations of the estimated model lead to the
- probability of membership in the reference group, a “success”
- slope coefficients that reflect changes in the odds for each unit increase in a predictor variable
Although this principles were illustrated for a logistic regression model with only a single predictor, the same principles apply to models with multiple predictors.