In practice, regression models typically have at least several predictor variables, called features in the language of machine learning. Bring additional information to the model in the form of additional predictors to increase fit and understand the relations of the predictor variables to the target.
5.1 The Model
5.1.1 Multiple Features
Here, introduce regression models with more than a single predictor.
Write the general, linear multiple regression model, here with \(m\) predictors or features:
\[\hat y = b_0 + b_1x_1 + b_2x_2 + \ldots + b_mx_m\]
The criterion of minimizing the sum of squared residuals for estimating the values of the \(b\) coefficients applies regardless of the number of features. Choose parameter estimates — \(b_0\), \(b_1\), \(b_2\), … — that minimize: \[\Sigma (y_i - \hat y_i)^2 = \Sigma e_i^2\] Chosen correctly, adding additional predictor variables tends to diminish the size of the residuals as corresponding model fit improves. Improved fit yields increased:
- Predictive accuracy
- Understanding of relationships
The number of predictor variables, features, in a model depends, in part, on its goal. Models built for explanation and understanding of the relationships among the variables tend to have two or three to six or so predictor variables. The emphasis here is on interpreting the slope coefficients.
Models built solely to maximize predictive accuracy begin with as many predictor variables as possible. If available, an initial model may start with hundreds of predictor variables. However, there are techniques to filter out features that do not contribute much to predictive accuracy, both before and after formal analysis of the model. Usually, however, after a set number of useful features have been included in the model, adding more features does not increase predictive accuracy nor understanding.
5.1.2 Ceteris Paribus
One of the most essential concepts in all of science and analysis in general is establishing a causal relationship. Does the variable \(x\) cause variable \(y\)? For example, does decreasing the price of a product lead to more sales? Does implementing the new quality control procedure maintain the same level of quality at less cost?
Three conditions must be fulfilled to establish a causal relationship.
- The variables must be related.
- Any changes in the value of variable \(x\) must lead to a change in variable \(y\) that occurs after the change in the value of \(x\).
- Changes in \(x\) directly lead to changes in \(y\) without other variables creating the relationship between \(x\) and \(y\).
Correlation does not imply causation. Yes, the more fire trucks at that the fire, the more damage results from that fire. However, fire trucks do not cause damage. Instead, there is another variable that causes both the Number of Fire Trucks and the Fire Damage, which is the Severity of the fire.
The Number of Fire Trucks at the fire is highly correlated with Fire Damage. A regression analysis would likely show a significant slope coefficient relating just the two variables. However, because Fire Severity is a confounding variable in this relationship, Number of Fire Trucks does not case Fire Severity. Fire Severity is the causal agent in this situation.
Establishing a causal relation between requires eliminating all potential confounding variables that could be causes but are not. Running a formal experiment with randomization is the best way to proceed but multiple regression provides information that controls for other confounding variables. The slope coefficients in a multiple regression model have a special meaning that extends beyond the meaning of a slope coefficient in a single predictor model.
Partial slope coefficient \(b_j\) isolates the relation of predictor \(x_j\) to response \(y\) with effects of the remaining predictor variables held constant. Control eliminates the impact of confounding variables This concept of holding the values of other variables constant has its own erudite reference.
The estimation of the effects of a unit change in each predictor variable on the response variable applies the concept of ceteris paribus. The value of all other predictor variables are held constant regarding the impact of the corresponding feature \(x_j\) on target \(y\).
Holding the values of the other variables constant provides for statistical control, which mimics the equivalence attained with experimental control.
Changing the value of a single variable, \(x_j\), increasing by a single unit, also changes the values of all variables correlated with \(x_j\). Multiple regression eliminates the impact of confounding variables. The result is the analysis of the direct impact of the variable of interest, free of confounding variables. How is this accomplished?
Unless all the predictors correlate zero, the partial slope coefficient for \(x_j\) does not equal the corresponding slope coefficient when \(x_j\) is the only predictor. To what extent does the size of slope coefficient \(b_j\) indicate the direct impact of \(x_j\) on the target, and to what extent that the coefficient indicates the impact of variables correlated with \(x_j\)? Consider the following examples.
5.1.2.1 Selling Price of a House
Suppose a Realtor studies the relation of the size of a house to its selling price. To investigate, realize that the following models yield different estimates for \(b_{size}\), the slope coefficient for the size variable, \(x_{size}\).
\[ y_{Price} = b_0 + (b_{size})x_{size}\] \[\textrm{vs}\] \[y_{Price} = b_0 + (b_{size})x_{size} + (b_{age})x_{age}\]
In the first example of a single predictor model, \(b_{size}\) indicates the direct impact of Size on Price as well as the impact on Price of all variables correlated with Size. For example, newer homes tend to be larger than older homes. The size of the house and age of the house correlate positively if age is the year constructed. Both influences are realized in the magnitude of \(b_{size}\) in the single predictor model. Increase the value of \(x_{size}\) by one unit and the value of \(x_{age}\) also increases.
The multiple regression model partials out the impact of Age on Price, which is held constant. The size of \(b_{size}\) in the multiple regression model differs from that of the single predictor model which does not explicitly consider the impact of Age.
Holding the age of the house constant means that the partial slope coefficient \(b_{size}\) indicates the impact of size on selling price for houses of all the same age.
In the multiple regression model, \(b_{size}\) represents the impact of Size on Price free from the correlated impact of Age.
5.1.2.2 Gender and Salary
A legal assessment of the relationship of Gender to Salary at a company demonstrated that men, on average, made more than women in comparable positions. That is, \(b_{Gender}x_{Gender}\) is significantly different from zero in the following regression equation.
\[y_{Salary} = b_0 + (b_{Gender})x_{Gender}\]
However, \(b_{Gender}\) reflects both the direct impact of Gender on Salary as well as the impact of any variables correlated with Gender. To assess a more relative direct effect of Gender on Salary, use multiple regression to control other potentially related variables such as years of work experience. Otherwise, if the company more recently hired more women than men, salaries could be less for these women because of less work experience.
\[y_{Salary} = b_0 + (b_{Gender})x_{Gender} + (b_{Years})x_{Years}\]
Holding work experience constant means that the partial slope coefficient \(b_{Gender}\) indicates the impact of evaluating the effect of gender on salary for a group of employees who all worked at the company the same amount of time.
In this situation, men and women who worked at the company for any given number of years, such as three, would earn the same average salary. If, in fact, more women were recently hired than men, then the slope coefficient \(b_{Gender}\) from the multiple regression model may no longer be significant, reducing in size to a value close to zero.
5.1.2.3 Assessment of Causality
Interpretation of partial slope coefficients provides much context for understanding the relations among the variables. With the influences of potentially confounding variables partialled out, partial slope coefficient assists the evaluation of potential causality. If all potential confounding variables were held constant, then the direct effect of the feature on the target variable would be realized by the size of the corresponding partial slope coefficient.
Of course, the problematic assessment is “If all potential confounding variables were held constant”. Some potentially confounding variables may not be measurable, and others may be unknown. To truly assess causal relationships requires experimental control with randomization of units such as employees into groups, followed by an experimental intervention. For example, after randomization, the groups receive differing amounts of a drug in a medical experiment, or receive different teaching strategies in an educational experiment.
Still, holding the values of some known confounding variables constant in a multiple regression analysis can usefully separate their impacts on the response variable \(y\). This concept plays a central role in the general application of regression analysis, but is not necessarily of primary interest if the ultimate goal is only predictive efficiency.
5.2 Feature Selection
Given that the model includes multiple predictor variables (features), typically some predictor variables – features – are more useful than others. Some features may not be useful at all. A major task of building multiple regression models is deciding what features to include in the model. How best to choose which predictors to include in the model?
In general, select the features for a model according to these guidelines.
Choose predictor variables that satisfy the following two conditions:
1. Unique Information: A proposed predictor variable does not highly correlate with the predictor variables (features) already in the model.
2. Relevant Information: A proposed predictor variable correlates with the target \(y\).
Ideally, each predictor variable relates to \(y\), but not to the other predictors, X. Each additional predictor variable ideally contributes new and relevant information to the understanding of the value of \(y\).
5.2.1 Parsimony
Data costs money. The fewer variables in the model, the less expensive to deploy the model. The goal is to balance the needs of accurate prediction with minimal expenditure and maximum simplicity. To construct a model, select the features that balance model fit with the smallest feasible set of predictor variables.
Adding additional predictors (features) to an already parsimonious model would only incrementally increase fit of no practical importance. Further, adding highly correlated features can detract from the estimation of individual partial slope coefficients.
Feature selection can pare down a large data set with potentially hundreds of features to a more manageable size. The more variables in the model, the more machine time to estimate the model. Computation time is trivial for a small model and data set, but potentially considerable even with powerful computers for a data set with hundreds of thousands if not millions of rows of data (samples).
5.2.2 Correlations
A standard technique for viewing the structure of the relationships among the variables in the model is to construct a table of their correlations.
The structure of the correlation matrix reflects two standard properties of correlations.
- Each variable correlates with itself perfectly, \(r_{xx} = 1.0\).
- The correlation of two variables is symmetric, \(r_{xy} = r_{yx}\).
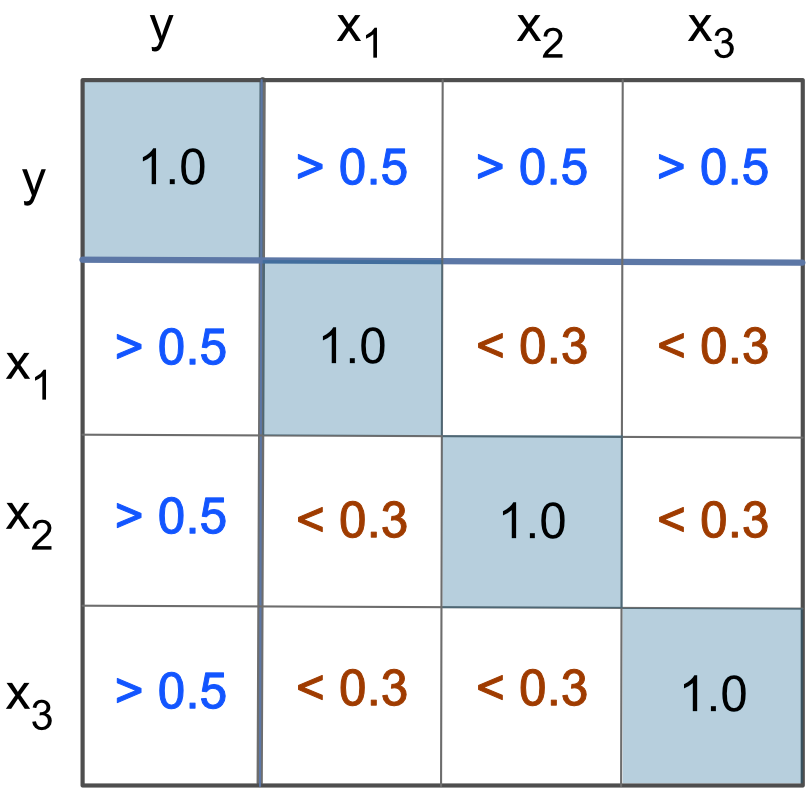
The main diagonal of a correlation matrix, shown in Figure 5.1, from the top-left to the bottom-right corner, consists of 1.00’s. The region above the main diagonal, the upper-triangle, has the same correlations as the region below the main diagonal, the lower-triangle. For this reason, a correlation matrix may be shown only with the lower- or the upper-triangle.
Figure 5.1 shows the relationships among the model variables that would lead to a successful model for prediction, serving as a heuristic guide to feature selection. The correlations of the predictor variables with the target are larger than 0.5, so each predictor is relevant. Further, the correlations of the predictor variables with each other are all less than 0.3, so each predictor provides at least some unique information.
A heuristic is a “rule of thumb”, a general guideline for decision making that does not offer precise, analytical guidance but does provide useful, reasonable information.

The values of 0.5 and 0.3 are practical but not necessary thresholds. The larger above 0.5, and the smaller below 0.3, the better. Ideally, all feature-target correlations would be above 0.9, and all correlations between each of the features would be below 0.1. Unfortunately, this more extreme version typically does not occur in practice, and many successful models do not strictly satisfy even the 0.5 and 0.3 guidelines.
The correlation among the predictor variables can tend to be higher than 0.3 for a useful model if the predictors are all relevant regarding the target variable.
Regardless of the size of the correlations among the predictor variables, the formal, analytic statistic for evaluating their relationships with each other is tolerance discussed in Section 5.3.1.
Also, the strength of the relationship depends on the magnitude of the correlation, not the sign. So the same principles apply to negative correlations. A predictor variable that correlates negatively with the target is relevant when the correlation is less than -0.5 or so. Two negatively correlated predictor variables tend to yield non-redundant information when their correlation is greater than -0.3.
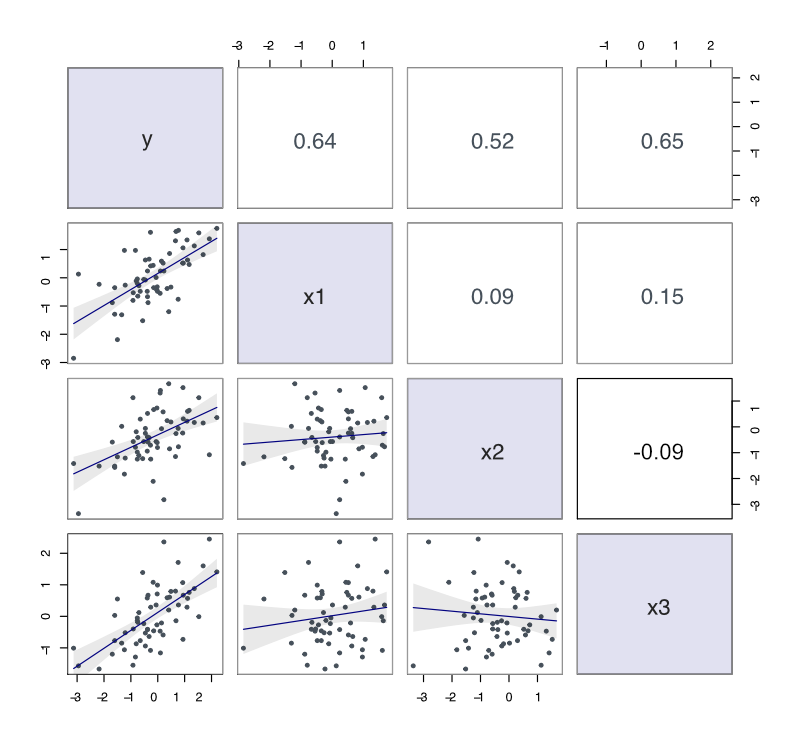
Modern computer technology provides for a visualization of the correlation matrix. One possibility follows.
Figure 5.2 provides an example of scatterplot matrix from actual data that follow the desired pattern shown in Figure 5.1. Each feature offers at least some unique information because all correlations among the features are at 0.30 or less. Each feature is relevant because all feature correlations with the target are above 0.50.
Another visualization of a correlation matrix follows.
Figure 5.3 presents an example of a correlation matrix heat map.
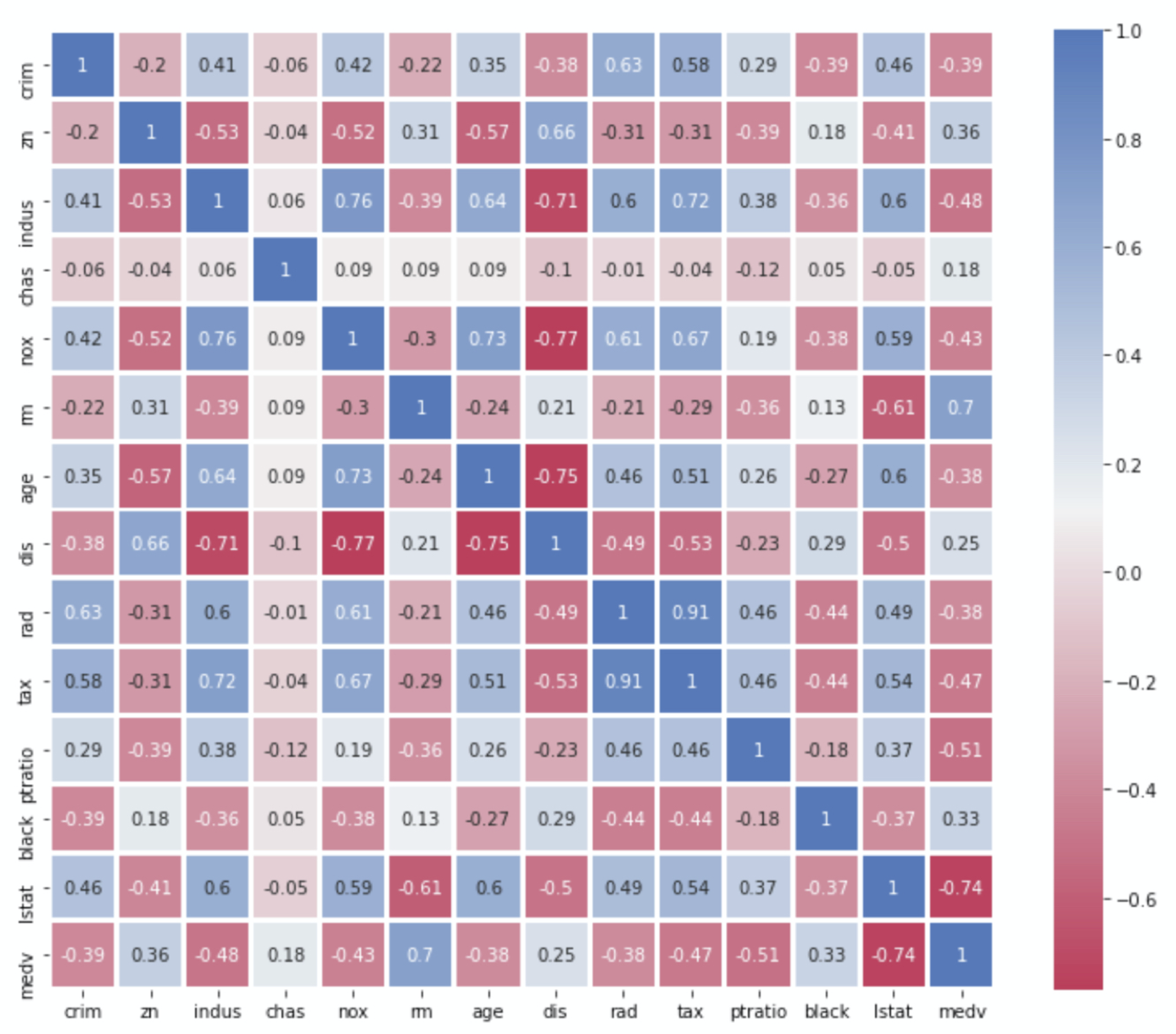
Viewing the correlation matrix and/or heat map of the relationships between each of the model variables provides much information to assist in constructing the final model.
5.2.3 p-values
Each slope coefficient is evaluated against the null hypothesis that the corresponding variable is not related to the response variable. If the null hypothesis that the corresponding population slope coefficient equal 0, \(\beta_j=0\), is true, the computed sample slope coefficient, \(b_j\), should be approximately equal to 0 but not exactly. So the evaluation of the null hypothesis is the evaluation of how close \(b_j\) is to 0. Too far from 0, about two standard errors, indicates a surprising result if the null hypothesis of \(\beta_j=0\) is correct. For predictor variables with a \(p\)-value > \(\alpha = 0.05\), no relationship was detected, the result is consistent with \(\beta_j=0\).
An informal but potentially misleading feature selection process simply drops all variables from the model that had \(p\)-values larger than 0.05. The advantage of this selection technique is simplicity. The disadvantage is too much simplicity, but can be somewhat worthwhile in the absence of more sophisticated techniques. However, if two predictor variables or features are highly correlated, as shown in the following section, neither feature may have a small \(p\)-value, yet one of the variable should be retained. As such, more sophisticated analyses of feature selection described next are recommended over the \(p\)-value approach.
5.3 Collinearity
A useful property of a feature (predictor variable), uniqueness, specifies that a feature does not correlate (much) with other features. To the extent that features correlate with each other, they are redundant, and this redundancy presents two issues. First, adding redundant features to a model does not increase predictive accuracy to any practical extent. Second, there is a problem with the interpretation.
Collinear predictor variables provide redundant information regarding the target variable \(y\). Collinear predictor variables do not decrease predictive accuracy, so not an issue if there no intent to interpret the coefficients. However, as previously indicated, in most analyses the goal is to achieve predictive accuracy with at least some understanding as to the relative impact of the different predictor variables.
What is the influence of collinearity on the estimation of the regression coefficients, the intercept and slope coefficients? Estimation of the corresponding partial slope coefficients follows the principle of holding the values of the other predictor variables constant. When both predictor variables represent different names for more or less the same concept, their estimated standard errors are inflated because their effects on \(y\) cannot be easily disentangled from each other.
To illustrate, consider an extreme case. The following example includes two almost perfectly correlated predictor variables. Management seeks to understand the factors that contribute to the maintenance costs of its machines used to manufacture its product. One consideration is the number of days a machine runs until a breakdown occurs. At a meeting to discuss the various possibilities, one manager suggests that the Age of the machine is a contributing factor. Another manager suggests that the Time required to manufacture the product since the machine was purchased is the critical variable. During any given week, a machine could be idle most if not all of the time. Yet another manager suggests simultaneously studying both variables.
Read the data into the R data frame d from the web. Do the multiple regression analysis that predicts Days until breakdown as a function of Age and time the machine has been Used.
f <- "http://web.pdx.edu/~gerbing/data/collinearity.csv"
d <- Read(f)
reg(Days ~ Age + Used)The data consists of the following ten samples (observations, rows of data, cases, examples, instances).
> d
Age Used Days
1 2014 1833 703
2 1938 1739 1214
3 2289 2072 1271
4 1447 1202 20
5 1831 1790 169
6 1293 1117 39
7 2014 1739 466
8 1889 1740 707
9 1889 1669 941
10 1889 1748 5605.3.1 Collinearity Indices
The most straightforward approach to detecting collinearity examines the correlations among the features. Find these correlations in the Regression() output. This example presents an extreme collinearity as \(r_{age,used}\) equals 0.97 to within two decimal digits.
Correlations
Days Age Used
Days 1.00 0.79 0.73
Age 0.79 1.00 0.97
Used 0.73 0.97 1.00The primary limitation of using correlations to detect collinearity is that, by definition, a correlation coefficient is a function of only two variables. Collinearity, however, results from any number of linearly related predictor variables. In practice, detect many instances of collinearity by examining the correlations.
A more sophisticated approach to detecting feature redundancy among the predictors, the features, follows. Create a regression model for each predictor in which the predictor becomes the target or response variable, and all remaining predictors are the predictor variables for this model. Refer to a particular feature as the \(jth\) feature. If \(x_j\) is collinear with one or more of the remaining predictors, then the resulting \(R^2_j\) should approach 1.
When doing a regression analysis with the target of interest, \(y\), the closer \(R^2\) is to 1, the better the model fit. However, when doing a regression of one feature on all the other features, we want a poor fit. That is, the other predictor variables should do not do well predicting \(x_j\). If there is no collinearity, then \(R^2_j\) should approach 0 because the remaining features have little information regarding \(x_j\). Low collinearity of feature \(x_j\) implies that it brings relatively unique information to the prediction of the true target of interest, \(y\).
This value of \(R^2_j\) becomes the basis for defining statistics to assess collinearity for each predictor.
Subtracting \(R^2_j\) from 1 implies that the desirable value of tolerance is high, indicating little overlap of \(x_j\) with the remaining predictor variables. Low tolerance values indicate collinearity, with the value of 0.2 and lower usually chosen as a heuristic guide to indicate excessive collinearity.
From the tolerance statistic comes another collinearity statistic.
The minimum value of VIF is 1, which indicates no collinearity. Values larger than 1 indicate the extent of inflation of the variance, the square of the standard error of the variable’s slope coefficient. A VIF of 2, for example, indicates that the variance has doubled over the state of no collinearity.
If \(R^2_j\) is as high as 0.8, tolerance is 0.2 and VIF\((b_j)\) is 5, which is generally considered the more or less arbitrary cutoff for collinearity. Larger values of \(R^2_j\), which indicate higher levels of collinearity, result in higher values of VIF.
The assessment of collinearity contributes to feature selection by deleting predictors with high collinearity. Of course, do not delete all predictors with high collinearity. Once one variable is gone, another variable with which it was highly correlated may not correlate much with the remaining predictor variables.
5.3.2 Example
Model Days (to breakdown) as a function of Age and (Time) Used.
For multiple regression, separate the predictor variables by plus + signs.
f <- "http://web.pdx.edu/~gerbing/data/collinearity.csv"
d <- Read(f)
reg(Days ~ Age + Used)Model Coefficients
Estimate Std Err t-value p-value Lower 95% Upper 95%
(Intercept) -1888.461 695.105 -2.717 0.030 -3532.124 -244.799
Age 2.435 1.548 1.573 0.160 -1.226 6.096
Used -1.205 1.532 -0.787 0.457 -4.827 2.417 The estimated multiple regression model to predict the number of days between Breakdowns from the Age in days and the number of days the machine is Used is, \[\hat y=-1888.46+2.44 x_{Age}-1.21 x_{Used}\]
Model Fit
Standard deviation of residuals: 298.743 for 7 degrees of freedom
R-squared: 0.657 Adjusted R-squared: 0.559 PRESS R-squared: 0.172
Null hypothesis that all population slope coefficients are 0:
F-statistic: 6.703 df: 2 and 7 p-value: 0.024 Collinearity
Tolerance VIF
Age 0.051 19.657
Used 0.051 19.657☞Any collinearity problems? Why or why not? The output indicates much collinearity because tolerance for both predictor variables, Age and Used, is only 0.051, considerably below the informal cutoff of 0.2. Given this tolerance value, the variance inflation factor, VIF, is necessarily much above 5, here as large as 19.657.
The accuracy of predictability using this model is a considerable improvement over using no model at all, as indicated by \(R^2=.66\) and \(R^2_{adj}= .56\). Unfortunately, the high collinearity leads to unstable estimated slope coefficients \(b_{Age}=-2.44\) and \(b_{Used}=-1.21\), evident from their respective standard errors, 1.55 and 1.53. These estimates result in extremely wide 95% confidence intervals of -1.23 to 6.10 and -4.83 to 2.42 (for \(t_{.025} = 2.26\) at \(df=9\)), respectively.
With 95% confidence, each population slope coefficient \(\beta\) likely lies anywhere within the corresponding large interval. Both intervals include 0, so do not reject the null hypothesis of no relation to the target. Neither population regression coefficient may be differentiated from zero.
Age of machine, and Time the machine was used, are almost perfectly correlated, \(r=0.97\). Using both of these variables as predictors in a regression model to predict the time until the next machine breakdown results in a collinear model. Tolerance is well below the arbitrary cutoff of 0.2, with the corresponding VIF well above 5. The estimated slope coefficients are unstable because the model attempts to portray the separate effects of each predictor variable on time between Breakdowns. Yet the two predictor variables are essentially two names for the same concept. Using both predictors simultaneously in the model does not improve the accuracy of prediction over the use of either one of the variables alone. It also yields highly unstable, unusable estimates of the resulting slope coefficients.
5.3.3 Remove Collinearity
One method to remove collinearity deletes all but one of the collinear predictor variables from the model. In this example, delete either Age of machine or Time the machine has been Used. Do not use both predictor variables simultaneously.
Another possibility forms a composite score of the collinear variables, such as their sum or their mean. Because the collinear predictor variables nearly indicate the same concept, their sum or mean summarizes that concept. With this method, all the information in the collinear variables is retained as their composite.
Here, examine the estimated model with one of the features deleted.
reg(Days ~ Age)Age only: Days (to breakdown) as a function of Age
Output follows.
Model Coefficients
Estimate Std Err t-value p-value Lower 95% Upper 95%
(Intercept) -1700.364 636.930 -2.670 0.028 -3169.128 -231.601
Age 1.249 0.341 3.664 0.006 0.463 2.035 With just Age as a predictor, now its slope coefficient is significantly different from zero, with \(p\)-value \(=0.006 < \alpha=0.05\).
Model Fit
Standard deviation of residuals: 291.537 for 8 degrees of freedom
R-squared: 0.627 Adjusted R-squared: 0.580 PRESS R-squared: 0.487
Null hypothesis that all population slope coefficients are 0:
F-statistic: 13.428 df: 1 and 8 p-value: 0.006 Here drop the other feature.
Used only: Days (to breakdown) as a function of time Used
Model Coefficients
Estimate Std Err t-value p-value Lower 95% Upper 95%
(Intercept) -1292.922 634.358 -2.038 0.076 -2755.755 169.910
Used 1.142 0.376 3.038 0.016 0.275 2.009 With just time Used as a predictor, now its slope coefficient is significantly different from zero, with \(p\)-value=0.016 \(< \alpha=0.05\).
Model Fit
Standard deviation of residuals: 325.100 for 8 degrees of freedom
R-squared: 0.536 Adjusted R-squared: 0.478 PRESS R-squared: 0.384
Null hypothesis that all population slope coefficients are 0:
F-statistic: 9.232 df: 1 and 8 p-value: 0.016 Following are the corresponding separate regression models for predicting the number of days between Breakdowns from the Age in days or the number of days the machine is Used. \[\hat y=-1700.36 + 1.25 x_{Age} \] \[\hat y=-1292.92 + 1.14 x_{Used}\] The fit index from these one-predictor models is reasonable; it is equivalent to the precision obtained from the multiple regression model, as indicated by the respective \(R^2_{adj}\) of .58 and .48. The estimated slope coefficients \(b_{Age}=1.25\) and \(b_{Used}=1.14\) are considerably more stable, given the dramatically reduced standard errors of .34 and .38, respectively. The considerably smaller 95% confidence intervals around the estimated slope coefficients, again computed from \(t_{.025} =2.26\) for \(df=9\), are, respectively, 0.46 to 2.04 and 0.28 to 2.01.
5.4 Best Subsets
The lessR package includes the data values analyzed here as part of the Employee data set. How is Salary related to other variables in the data set? One feature is Years employed at the company. Another two features are scores on a Pre-test and, following instruction in some legal topic, a Post-test.
Run the regression analysis on the lessR data set Employee.
d <- Read("Employee")
reg(Salary ~ Years + Pre + Post)The scatterplot/correlation matrix reveals the qualitative results of the regression analysis. The target, \(y\), correlates 0.85 with Salary and virtually 0 with the test score variables. Moreover, much collinearity with the test scores, which correlate 0.91. There will be only one significant predictor in this analysis, and only one test score would remain (or their average) if they would relate at all to the target, but neither does, so none remain in the final model.
Estimate Std Err t-value p-value Lower 95% Upper 95%
(Intercept) 52269.406 14759.452 3.541 0.001 22205.385 82333.426
Years 3289.118 366.884 8.965 0.000 2541.798 4036.437
Pre -164.842 434.322 -0.380 0.707 -1049.527 719.844
Post 161.756 441.110 0.367 0.716 -736.754 1060.267The information in the scatterplot matrix and the coefficient estimates provide actionable information for revising the model. Which features are relevant? Which features are redundant (collinear)? Which slope coefficients cannot be differentiated from zero? All useful information, but the natural follow-up question is how well would a revised model perform?
One way, of course, to evaluate a revised model is to analyze a proposed model. A more general procedure evaluates a set of revised models.
To help decide which variables to drop from the model, directly view how fit changes as different features are deleted.
Choose the most parsimonious model, which balances the one of the best, if not the best, fit with the minimum needed number of predictor variables in the model.
The output of Regression() provides the fit index \(R^2_{adj}\). The \(R^2\) statistic always increases when adding an additional predictor to the model, or, conversely, necessarily decreases if the analyst removes a predictor. This increase or decrease always occurs even if trivial when the predictor is either not relevant and/or not unique. \(R^2_{adj}\), instead, can actually decrease if a useless predictor is added to the model, or increase if a useless predictor is removed. \(R^2_{adj}\), then, serves as a more realistic fit index than \(R^2\) for comparing different regression models.
As previously indicated, when deciding which variables to delete, the goal is not always to select the model with the best-possible fit. Instead, balance the number of features (predictor variables) with fit. Usually pursue the most parsimonious model, which may sacrifice a negligible amount of fit to the data from which the model was constructed for a simpler model more likely to generalize to new data.
For the subset analysis in the current example, scan the \(R^2_{adj}\) statistic for the various models. With only three predictors there are eight possible model combinations of either including or excluding a feature from the model. The model with all three predictors does not even appear in the output as combinations of predictors that generate a negative \(R^2_{adj}\) are not considered.
Years Pre Post R2adj X's
1 0 0 0.718 1
1 1 0 0.710 2
1 0 1 0.710 2
1 1 1 0.702 3
0 1 1 -0.014 2
0 0 1 -0.026 1
0 1 0 -0.028 1
[based on Thomas Lumley's leaps function from the leaps package]☞Based on this information and the best subset analysis, which model do you recommend? Why? Given the large collinearity and the best subsets regression, the best-fitting model here is the model with only a single predictor variable, Years, with \(R^2_{adj}=0.718\). Adding more predictors decrements fit, so the most parsimonious model is the obvious choice for these data and variables.
In this example, the best-fitting model is also the most parsimonious model, which makes model selection particularly straightforward. More generally, the best-fitting parsimonious model may have a slightly lower \(R^2_{adj}\) than a model with more variables. The cost of a slight decrease in fit, however, is worth jettisoning the additional variables to achieve a simpler model, less likely to overfit.
Parsimony is an effective strategy to build models that successfully generalize to new data for actual predictions, less likely to take advantage of random, arbitrary fluctuations in the data from which the model is estimated.
Of course, adding more predictor variables to the model dramatically increases the number of possible combinations of subset models. With too many predictor variables to conveniently list all possibilities, the algorithm selects reasonable subsets of all possible subset models.
5.5 Summary
5.5.1 Context
Construct a model, a prediction equation, that predicts the value of response variable or target y from a set of input values of one or more predictor variables or features X, such as \(x_1\), \(x_2\) etc. The traditional terms for \(y\) and X are response variable and predictor variables. Such a model is also an example of what is called supervised machine learning, which defines the equivalent terms of target and feature. The language refers to the same concepts with different names.
In terms of notation, \(y\) is lowercase because there is only a single variable whose values are predicted. Of course, \(y\) and X are generic names for the names of what become in a given analysis the names of specific variables, such as \(x_{Weight}\) and \(y_{MPG}\). And, of course, in the modern world of computers, the computer performs all the following steps.
5.5.2 Construct
The steps in building a predictive model with linear regression analysis and applying to prediction follow.
Gather data for variables X and \(y\), organized into a standard data table.
Input the data table into a regression analysis function, such as
Regression()provided by my R package calledlessR, one of the more comprehensive (and free) linear regression functions available anywhere.For the default linear model, apply regression analysis of the data to estimate the parameters of the prediction model, \(b_0\) for the y-intercept and slope \(b_1\) for \(x_1\), slope \(b_2\) for \(x_2\), and so forth for all the individual predictor variables. Of course, for a specific model estimated from a give data table, the value of each \(b_j\) is a specific number.
With the subsequent linear equation, such as with two predictor variables, calculate the fitted value, \(\hat y\) as follows. \[\hat y = b_0 + b_1(x_1) + b_2(x_2)\] For the given data on which the model learned the values of the parameters, compute the fitted value, \(\hat y\), for each row of data in the data table. This computation is possible because the values of \(y\) in the data from which the model is estimated are already known, required to estimate the relationship between the X variables and \(y\).
Evaluate the fit of the model by assessing how close the actual data values, \(y\), are to the corresponding fitted values, \(\hat y\). For each row of the data table, calculate the residual, the difference between what is, \(y\), and what is fit by (consistent with) the model, \(\hat y\). \[e = y-\hat y\] From the column of residuals, the values for computed variable \(e\), calculate the fit indices \(s_e\) and \(R^2\).
With multiple predictor variables or features, do model selection, usually drop some of the predictors from the model because they do not contribute to model fit. A four predictor variable may be just as accurate in predicting values of \(y\) as a seven predictor model. Once the initial model is constructed, do additional analyzes to discover a potential subset model, selected to achieve parsimony, a balance between model fit, and ultimately prediction accuracy, and number of predictor variables.
If a parsimonious model fits at least reasonably well, apply the model to new data to predict unknown values of the target, \(y\), from the known values of the X variables. In this situation with an unknown value of \(y\), the value fitted by the model, \(\hat y\), is a true _prediction.
Place a prediction interval about the predicted value, \(\hat y\), to specify a range of values that likely will contain the actual value of \(y\) when it occurs.
5.5.3 Interpretation
A task related to but separate from prediction per se is the interpretation of the values of the estimated parameters, \(b_j\). For each 1-unit increase in the value of (each) \(x_j\), the corresponding data value \(y\) will, on average, change by the corresponding slope coefficient \(b_j\), with the values of all other predictor variables held constant.
Interpreting the value of each \(b_j\) estimated from the data applies only to that particular data set from which the model was estimated. Use inferential statistics to generalize the value of each \(b_j\) to the population.
Conduct a hypothesis test of the null hypothesis of no relation to see if there is a relationship between \(x_j\) and \(y\) (with the values of all other \(x\)’s held constant).
If there is a relationship indicated by rejecting the null hypothesis, construct the confidence interval for the slope coefficient \(b_j\) to estimate its value in the population from which the sample data was derived.