|
pictures of the week |
thought-bite of the week: "Even when nature does not produce the same species in analogous climates,… we still noticed a striking resemblance of appearance and physiognomy in the vegetation of the most distant countries.… [R]eason cannot stop man forming hypotheses on the origin of things"(Humboldt, "Personal Narrative", from Jaguars and Electric Eels, ed. & trans. Wilson, p. 13) |
|
mini-text of the week (start): "The destruction of the forests… forcefully explains why the present Lake Valencia is decreasing.…"Humboldt, "Personal Narrative", from Jaguars and Electric Eels, ed. & trans. Wilson, p. 31 (read more) |
|
√ |
(5') Thought-bite of the week: Now that everybody (?) is on board the Humboldt SINQ Canoe, we'll get to the "sustainable environmentalism" part. Key points: "noticing" (observing, gathering data) and "forming hypotheses" (what does it mean, taken all together? - an early stage of evolutionary theory). Mini-text of the week: a very early systematic explanation of environmental damage and climate change. This week's theme: plants, and also food. Followup on last week's issue of teachers getting into trouble doing math activities about slavery. |
|
+ |
(10') Linnaeus and the classification of life-forms. How scientists give those life-forms their names, and who chooses which scientists get to do that? (Fortey, Trilobite, p. ••) Ungraded quiz: Which life-forms do you recognize when you encounter their biological (Latin!) names? Can you see and smell the difference between quercus alba and quercus rufus? How about a nice plate full of Dosidicus gigas (aka diablo rojo)? Should we offer the Humboldt-named schools a lesson plan organized around a banquet of Humboldt-named plants and animals? Maybe with a fund-raiser? |
|
+ |
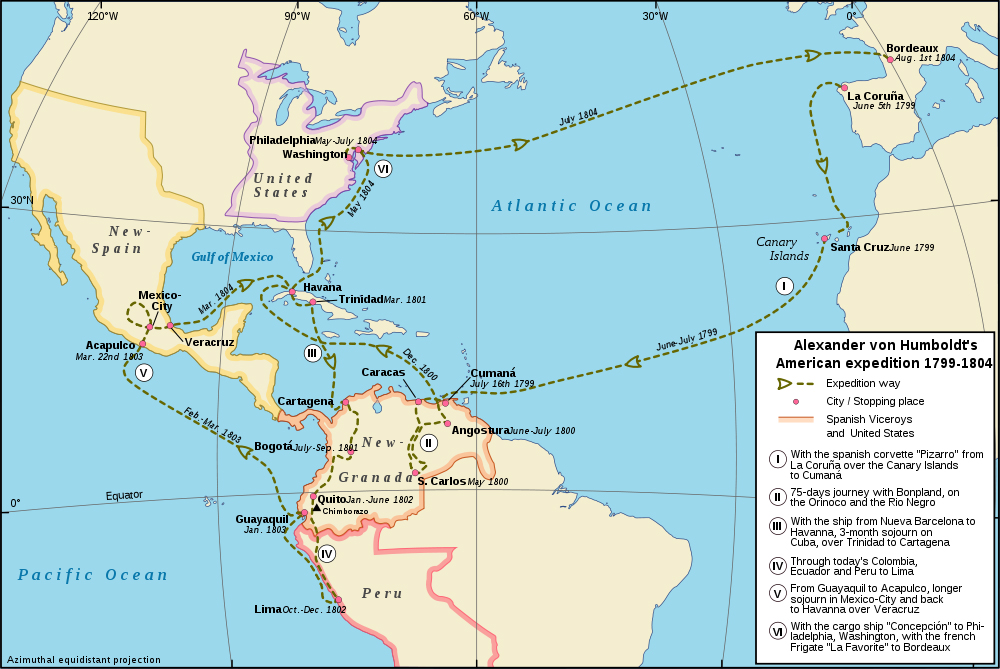
(20') SINQing the Humboldt canoe, so that we can then load it and travel safely in it. 1) "Brute force" solution: actually sinking a similar canoe - the key guy at the gym says it's OK to him; 2) "Semi-Brute Force Solution: "dry dock" simulation using Laura Dassow Well's description of Humboldt's canoe and its cargo of people, equipment, and various critters- we'll do that right in the classroom; 3) "Smart Person Solution" - review of previous meeting: saving time and sweat by (e-)pencil-and-paper calculation of volume and "ball park" estimation of weight and displacement. Our materials: Humboldt "canoes" made from quart carton (heavy cream) and orange juice can; "rivers" to float our canoes in (pitcher, yogurt container; water; rolls of pennies; brains and calculators (human or machine). First: What is the volume of that original Humboldt Canoe (40' long, 3' wide, semi-circular cross section throughout)? How about one with a 3' width, rectangular transom (1.5' high), and flat bottom? How about one with a triangular cross section (3' wide, with bottom (keel) as right-angle? How does that relate to how many supply and sample boxes they could get into the Canoe, how much wood is needed to make various shapes of containers, and what your airline carry-on baggage allowance is? Would(n't) this all be easier if we used the metric system? ••Maybe: Worksheet about volume, weight, and displacement. What does all this have to do with: "displacement"; getting up the Orinoco, through the Casiquiare Canal, and down the Amazon (see map above); the Whiskey Rebellion; the Mexican War; and the science and economy of then and ("interpreting the past") now? Use your computer/ smartphone map links and applications to trace AvH's route in South America, starting with his travel up the Orinoco and down the Amazon. See Helferich, p. 52 map, but be aware that some place names have been changed over time. |
|
- |
(10') Review and expansion of quantification activities, with application to food. A story that includes a story problem: How do nursing mothers do it? Rough calculation vs. precise calculation. Relation to food and energy needs of explorers. What did Lewis & Clark and the "Party of Discovery" Eat? (some other time: what ate them). How does that compare to your diet? How is nutritional research conducted - how do we get, so to speak, a window into the stomach? |
| √ |
(10') presentation (continuation) about educational standards and their parts in the course: 1) evaluating own education; 2) helping others to learn - how standards are used to develop curriculum (curricula?) and learning activities; 3) introduction of writing assignment #3. |
|
+ |
(10') about writing skills - the "Leaving Home" assignment, part II of comments I intend to supply this with posted written comments, with appropriate protection of privacy. |
|
√ |
(5') Writing assignment 3: Your education and how it compares to standards.• Due 6 February (Thursday) two weeks from when it was first assigned, which was last Thursday (24 January) |
|
√ |
(5') Preview of book review assignment: 1) purpose and chief features; 2) choice of books (with some additons to come, to cover more topics or allow for books from PSU/MultCo libraries or your own resources) |
|
√ |
(5') Checkups & Previews: 1) Does everyone have the main texts and know where to find assignments and deadlines? Has everyone read the Wikipedia article about AvH? Gotten well into Helferich and Eels/Jaguars? 2) Has everyone done the several questionnaires? (Intake experiences • Skills inventory I • Academic background & interests) 3) Next meeting: formation of project teams and survey |