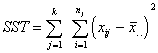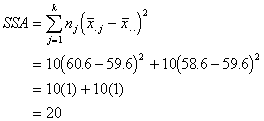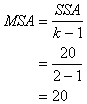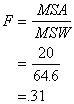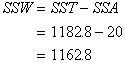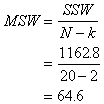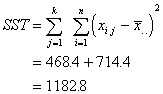lecture9

Lecture 9
Analysis of Variance

Two Groups
Analysis of Variance, commonly referred to as ANOVA (uh-nove-uh), is the same as a between groups t-test when used with two groups. It is a more general test, though, that allows one to compare several groups at once, not just two. Instead of using the t statistic as in the t-test, we use an F statistic. Why F? Because statisticians like to use letters to to abbreviate so that everyone else will be confused about what the heck they are talking about. That way they seem really smart. No, I'm mostly kidding. The letter F is a tribute to the inventer of ANOVA, Sir Ronald Fisher, knighted for his accomplishments in statistics. Fisher was a statistician who studied agricultural genetics among other things. It turns out that the F-test (or ANOVA) with two groups is equivalent to the t-test. You'll get the same result with either. But the ANOVA test is more general because it can be used in more complex studies that compare more than two groups.

In an earlier lecture, I described the t-test as a type of ratio--a ratio between the group difference and sampling variability (i.e., the standard error).

t = difference between groups
sampling variability

And I said the standard error is really based on the standard deviation, a measure of variability within the sample. ANOVA is really based on the same idea, but Fisher conceptualized it slightly differently. He thought of it as a ratio of two types of variances, the variance between group means and overall variance in the sample.

F = Variance Between Groups
Overall Variance

In the between groups t-test, we examined the difference between two means (). Another way to think of the difference between two means is as a type of variation among the means. Here we have just two means, but a difference is the same thing as a variation. (Remember the calculation of the variance of a group of numbers involves subtracting x from ?). If there are several groups, their group means may differ or vary. The overall variance is just the variation of scores in the sample. So, we could restate the F-test this way:

F = Difference Among the Group Means
Difference Among the Scores

If the differences between the group means is large relative to the amount of variability in the scores, the group differences are probably significant. If, however, there is a lot of variability in the scores, then the difference between (or among) the group means will not seem so large, a non-significant difference.

Notation
The notation in the formulas begins to get a little more complex with ANOVA, because we are planning on adding more groups. For some of you this is not a problem. For others, the subscripts are a little overwhelming. If so, click here for some detailed explanation of the notation.

Steps and Formulas for the Two-Group ANOVA
The steps for conducting are really the same as with the other tests. You need to know the hypotheses, then do the calculations to get the statistics, and then compare to the tabled value to see if there is a significant difference.

Because the ANOVA is conceptualized as a ratio of variances--hence the term Analysis of Variance, we need to compute the variance of the scores and the variance of the means. The variance of the scores is based on the Sum of Squares Within (SSW). The SSW is based on how the scores vary around the mean in each of the groups. The Sum of Squares Among the groups (SSA) is the squared deviations of the means from the total mean--how much the means vary from each other. If you put these two components togther, they add up to the Sum of Squares Total (SST). Here are the formulas:

Formula	Name	How To	Concept
	Sum of Square Total	Subtract each of the scores from the mean of the entire sample. Square each of those deviations. Add those up for each group, then add the two groups together.	This is just like computing the variance. The purpose is to find the deviation of all the scores from the middle. We haven't yet divided by how many there are, but we will.
	Sum of Squares Among	Each group mean is subtracted from the overall sample mean, squared, multiplied by how many are in that group, then those are summed up. For two groups, we just sum together two numbers.	This is a measure of how much the means differ from one another. Its conceptualized a little differently, because it is thought of as the variation of each mean from the mean of the total sample.
	Sum of Squares Within	Here's a shortcut. Just find the SST and the SSA and find the difference. What's left over is the SSW.	If we calculated the SSW from scratch, it would be the deviation of the scores in each group from its group mean, then added together. Represents variation within groups.

The next step is to turn each of these sums into averages. Just as when the variance is computed, we want the average deviation from the mean. So for these Sum of Squares, we want to divide by approximately how many things we summed up. The degrees of freedom is based on the number of groups or cases.

Formula	Name	How To	Concept
	Mean Square Among Groups	Divide the SSA by the number of groups minus 1.	Average of the sum of squares among the groups. Represents the amount of difference between the groups.
	Mean Square Within	Divide the SSW by the number of cases in the total sample minus the number of groups.	Average of the sum of squares within the groups. Represents the amount of variation of the scores within the groups.
There is no MST used

The F-test is just the ratio of the MSA and MSW:

F = MSA
MSW

It’s a ratio of the variance between the group means relative to the amount of variation in the sample (i.e., variation within each of the groups).

The Statistical Test
Next we need to make our decision about whether the groups are signfircantly different. Again, we calculate the F-test for the sample, then compare it to a table that tells us how extreme our sample F is relative to what we expect from other randomly drawn samples. To do that, we need a new table, Table G in the back of the book. To look up the value, we need to know the d.f. There are two, based on the numbers we used to divide the SSA and SSW. So, the numerator degrees of freedom is k - 1 (referring to the top MSA and the top part of the F ratio), and the denominator is N - k (referring to the MSW and the bottom part of the F ratio).

Example
Let's redo the t-test we did in the the one of the earlier lectures (Between Groups t-test). Remember the first born/second born example? Here's the data again.

Introvers-ion score First Born			Introvers-ion score Second Born
65	5.4	29.16	61	1.4	1.96
48	-11.6	134.56	42	-17.6	309.76
63	3.4	11.56	66	6.4	40.96
52	-7.6	57.76	52	-7.6	57.76
61	1.4	1.96	47	-12.6	158.76
53	-6.6	43.56	58	-1.6	2.56
63	3.4	11.56	65	5.4	29.16
70	10.4	108.16	62	2.4	5.76
65	5.4	29.16	64	4.4	19.36
66	6.4	40.96	69	9.4	88.36

The mean of all the 20 participants is .

Looking up in Table G under Numberator DF = 1 and Denomator d.f. = 18, the critical value needed for significance is . So, our test is not significant.

Relation between t-test and F-test
Before, I stated that the t and F-tests are equivalent. They will lead to the same answer. The number you caluclate is slightly different. It turns out that (or ). So, we should get the t-value we obtained before if we take the square root of F. .

Oops, this is not the t-value I obtained, but it is the t-value I should have obtained. Well, even your instructor makes mistakes! In the t-test example I made an error when calculating the pooled variance. I used the standard deviation instead of the variance, where and were called for in the formula. The error has now been corrected in that lecture. You should always be double checking my work, never trust your instructor!!--well maybe you shouldn't go that far.

Interpretation
The ratio of the among-groups variance to the within-groups variance was not large enough for significance. In other words, there was a non-significant difference between the groups. Thus, we assume, at least for the moment, that there is not a difference in the introvertedness of first and second born children in the population. If the F-test was significant, we would conclude the birth order does have an effect.

Three or More Groups
I'm not going to go into much detail about ANOVA with more than two groups , because the book gives an example of that. I do want to note a couple of things. ANOVA is sometimes referred to as an "omnibus" test, meaning that it is an overall test of differences among the means. When there are three or more groups, and we find significance among the group means, we do not know which groups are different from which. The overall, omnibus, test may be significant if just one mean is different from the rest. Or all group means may be significantly different from one another. A signficant ANOVA does not distinguish between these possibilites, it merely indicates there are some differences.

Alpha Inflation
So, often there are follow up tests conducted to see, specifically, which means are different from which other means. One way to do this would be to conduct some separate t-tests after one obtains a significant ANOVA, comparing two group means at a time. This is a big no-no in statistics. There are problems with this approach, although occaisionally one will see a published article that does this. One reason it is a no-no to conduct separate t-tests after a signficant ANOVA is because of something called alpha inflation. Alpha inflation (sometimes also called familywise error, or experimentwise error) occurs because multiple tests are conducted on the same data set. When too many tests are conducted, the original alpha value for each test is actually higher than expected (this is a probability thing). Instead of a=.05 it might actually be higher than that. This implies that the Type I error rate is higher than expected, and our chance of finding a significant difference in error is greater.

The remedy is to use a slightly modified version of the t-test to correct for the problem. There are a lot of these tests (often called post-hoc tests) out there. Some examples are the Bonferroni, the Scheffe, the Neuman-Keuls, and the Tukey. The Tukey test, also called the Honest Significant Difference test (HSD) is the best. The HSD compares all possible pairs of means withouth inflating alpha. Daniel provides a nice discussion of this test, so I'm not going to go over it here. So, if you need to find out which group means are different from one another, you should use the Tukey HSD test.

For an example SPSS output, click here.