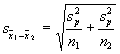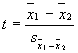Lecture
6
Between Groups t-test
Single Group Tests:
The z-test and the t-test
There are two tests that are used to see if a single sample mean is different
from the population mean, the z-test and the t-test. We've already discussed
the rationale for these under significance testing. The book provides more
detail on these tests and when they are used (Chapter 6). Frankly, they are
very rarely used, and I don't want to spend too much time on them.
One comment I do want to make is on
when to use which test. On page 165 of the Daniel text, there is a complex flow
chart that one can follow to make a decision about which to use. Actually, it
is much simpler than this. If the population standard deviation is known, use
the z-test. If it is not known, use the t-test. Because of the central limit theorem,
one doesn't have to worry about the normality of the distribution of the
population. In the flow chart, Daniel is pointing out, in part, that one has to
be cautious about using the single group t-test when there is a very small
sample size and the population is not normally distributed. Most of the time,
in real research, we don't know about the shape of the distribution of the
population, so people use the t-test regardless of whether the population
distribution is normal.
Between Groups
t-test
The between groups t-test is
used when we have a continuous dependent variable and we are interested in
comparing two groups. An example might be if there is experiment with an
experimental and control group, or perhaps a comparison between two non-experimental
groups like women and men. Another way to describe the situation in which the
between groups t-test is appropriate is to state that t-test involves a
dichotomous independent variable and a continuous dependent variable. Remember
that the independent variable is the one assumed to be the cause and the
dependent variable is the result or the outcome. The independent variable in
this case is group membership (e.g., gender is the independent variable). We
compare the means of the dependent variable for participants in the two groups.
So, the t-test is to see if the independent, grouping variable produces a large
difference between the means on the dependent variable.
I've already given you the
conceptual explanation of the two groups t-test in the previous lectures. To
reiterate a bit, it is a matter of checking to see if the difference between
two groups is one that is likely to occur by chance or not. If the means of the
two groups are large relative to what we would expect to occur from sample to
sample, we consider the difference to be significant. If the difference between
the group means is small relative to the amount of sampling variability, the
difference will not be significant.
We can think of the formula
conceptually as a ratio like this:
t
= difference between groups
sampling variability
When the value on the top of the
equation is large, or the value on the bottom of the equation is small, the
overall ratio will be large. The larger the value of t, the farther out on the
sampling curve it will be, and, thus, the more likely it will be significant.
The Standard Error
of the Estimate
The value that will be used on
the top of the t formula is simple. It's just the difference between the two
group means (
). Here x-bar with the subscript 1 denotes the mean of the
first group and the x-bar with the subscript of 2 denotes the mean of the
second group (of course, the subscript used has nothing to do with the actual
values used in the data set for the grouping variable).
The value on the bottom of the
equation is designed to gauge sampling variability. As in the previous
lectures, we estimate sampling variability with the standard error. The
standard error in this case can be more formally called the "standard
error of the estimate," because we are gauging the sampling variability of
an estimate of the difference between means. The standard error of the estimate
represents the standard deviation of the sampling distribution when the
sampling distribution is based on a large number of mean differences. You can
imagine a sampling distribution created by taking repeated samples of two
groups and computing the difference between the means in each.
Because we are not going to actually
construct a sampling distribution, we have to estimate the standard error. To
estimate the standard error, we use the standard deviation of the sample we
have. The standard deviation represents the variability of scores in the
sample. If we know something about how much scores in the sample tend to vary,
we can make a guess about how much variation we would expect in the sampling
distribution. Imagine drawing scores from a population with very low
variability. All the scores would be similar to one another, so the samples
drawn from that population would not vary much.
To make our guess at the standard
error of mean differences, we need to use the variability of scores within the
two groups. Because we have two groups, we need to find their variances and
"pool" them together. The variances of the two groups will be
symbolized by 
and 
where a 1 and a 2 are used as subscripts to denote the first or
second group. If we have those, we can pool them together in the pooled
variance estimate. Here's the formula, were 
represents the pooled variance
estimate:
n1 and n2 are the sample sizes for
each of the two groups. With the pooled variance, we can then estimate the
standard error. The standard error is symbolized by 
(like the symbol for the standard
error of the mean, but a subscript with the difference between the two means is
used).
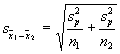
Now, all we need to do is to use
that value in our ratio, and presto, we have a t-test.
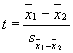
Well….almost.
The Statistical
Hypotheses for the t-test
At the beginning of the class, I
stated that we are interested in inferential statistics. We want to make
decisions about the state of the population, not just our puny little sample.
So, that means our real hypothesis concerns the population. The null hypothesis
with the between groups t-test is that the two groups are equal in the
population (either 
or 
, where m1 and m2 are the population means for the two
groups). In other words, if we could conduct our experiment on the entire
population, would we find a difference between the two groups? If we find
significance with our t-test, we conclude that there are differences between
the two population means.
How to Conduct the
Between Groups t-test
In our search for significance, we need to calculate our t-value and then see
if it will fall out on the end of the sampling distribution curve. The general
procedures that we will follow for calculating the between groups t-test is
very similar to the procedure we will follow for every other statistical test
we will conduct. Let me briefly summarize the steps in a table, then I'll
explain:
|
Step Number |
Description of Step |
Specific Example with Between Groups t-test |
|
1. |
Know the hypothesis you are testing |
|
|
2. |
Use the formula, finding the value of the standard error estimate first. In this case, the standard error is the pooled standard error that represents the sampling variation of the difference between two group means. |
|
|
3. |
Check to see if the calculated value indicates significance. To do this: determine the degrees of freedom, and look up the critical value in the table in the back of the book for alpha=.05 (in Daniel's tables, the subscript value .975 is used). If the value you calculated exceeds the value in the table, it is significant (i.e., the null hypothesis is rejected). |
d.f. = n1 + n2 - 2. |
|
4. |
Calculate the 95% confidence interval. Two values are used: (1) the low value, which subtracts the product of the critical value times the standard error, and (2) the high value, which adds that product. |
|
As with all tests we conduct, we
will compute a value and then compare it to a value in the table in the back of
the book. Note that Daniel calls the tabled value the reliability
coefficient. (Other books refer to it as the critical value or the tabled
value.) When we are making this comparison, we are looking to see how far out
on the sampling curve our sample is likely to be. Remember this picture?
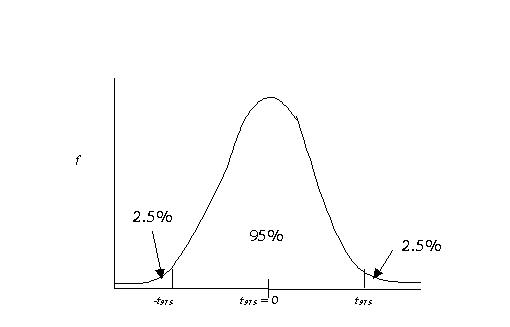
If our calculated value
exceeds the one in the table (i.e., the reliability coefficient), we have
significance. The reliability coefficient is denoted by t.975 when
alpha is equal to .05 and we are using a two-tailed test. More generally the
reliability coefficient will be referred to as t(1-a/2). We've decided to reject the null hypothesis
that the two groups were equal and we accept the alternative hypothesis that
states that they are different. This means that we can be 95% sure that the
differences between the two groups is not simply due to chance.
The Confidence
Interval
Some researchers also like to
compute a "confidence interval." The confidence interval is an
estimate of where 95% of the mean differences in the sampling distribution
should fall. It can also be stated as a representation of 95% confidence that
the population mean difference will fall within these two points. Remember that
our null hypothesis was that there is no difference between the population
means (
or 
). In the case of
the between groups t-test, when the intervals do not include 0, we have
significance. For example, if we are 95% confident that the difference between
the two groups in the population falls between 2.3 and 5.4, the difference
between m1
and m2
must be greater than 0, and thus there is a real (significant) difference
between the groups.
To calculate the confidence
interval, we find two values: the lower confidence limit (LCL) and the upper
confidence limit (UCL). These are obtained from values we already have, the
difference between our sample means, the tabled t-value (reliability
coefficient), and the standard error.
The next "lecture"
is an example with numbers.