Lecture
2
Sampling Distributions
Sample vs.
Population
Researchers distinguish between
samples and populations. A population is a large group of people to
which we are interested in generalizing. Examples might be: all people residing
in the U.S., all married females between ages 35 and 44, all children under age
3, all hospitals in the U.S. A sample is simply a smaller group drawn
from a population. For example: 1,000 people residing in the U.S., 120 women
between ages 35 and 44, 967 children under age 3, or 100 hospitals in the U.S.
A numerical summary of some kind,
such as an average, has two different forms: one form is used for the sample
and one form is used for the population. In Daniel's notation the average for a
sample is written as 
and the average for the population is written as m
(the Greek letter "mu"). The sample average () is a called a statistic and
m
is called a parameter. If you do not remember some of the other common
statistics and parameters, such as the mean, median, mode, standard deviation,
and variance, I suggest a review of Chapter 2 in the Daniel text.
Descriptive vs.
Inferential Statistics
Most people think of descriptive statistics when they hear the word
"statistics." For example, batting averages in baseball or "4
out of 5 dentists recommend…" But we are not really going to study that
type of statistics in this class. We are more interested in inferential
statistics, because those are the statistics that most researchers use. The
difference is that inferential statistics infer something about a
population, based on a smaller number of people, a sample. The whole enterprise
of inferential statistics is about making numerical guesses about a population
based on a sample. Descriptive statistics is merely for the purposes of
describing the sample. In descriptive statistics, results are not really meant
to apply to other samples or to the larger population.
Significance
Statistical significance is a particular term that researchers use.
Significance refers to a kind of certainty about whether or not some result in
a particular sample is a result that is likely to be true in population from
which it is drawn or other samples drawn from that population. For instance, if
32.1% of the sample report having not seen a doctor in the past year, how do we
know whether approximately 32% in the entire population has not seen a doctor
in the past year? Or, if a sample of employees in the Portland metropolitan
area have an average income of $37,189, how do we know if this result is likely
to be true if we surveyed all of the employees in the Portland metro area?
Now, one of the reasons why the
sample statistic might not be a good approximation of the population parameter
is that the sample was not a very good sample. That is, a small
unrepresentative sample was drawn for some reason. There are several ways to
draw samples for the population, some of them are good ways and some of them
are not so good. The better ways will produce samples that are representative
of the population (have all the same characteristics). For this class, we are
not going to discuss the methodology involved in drawing samples, and we will
assume that we have done a good job of that. For instance, a good way to draw a
sample is to take a random sample, in which every member of the population has
an equal chance of being selected for the sample.
Sampling
Variability
Even if we draw a perfectly
random sample, we are not very likely to get the same result in the sample as
we would in the population. Just by chance we are likely to get a somewhat
different set of folks in the sample, and this is called sampling
variability. Let's say we could pick 10 employees from the Portland metro
area perfectly by random. Let's also assume the mean income for all of Portland
metro employees is $37,189. It is very unlikely that the average income of the
10 people in our sample is going to be exactly $37,189. We might, for instance,
pick 10 employees from fast food restaurants completely by chance. Their
average income might be only about $10,000. Or we might get a sample of
lawyers, doctors, and cooperate executives by chance, and their average income
might be $157,000. It's probably pretty unlikely we would draw either of these
samples because they are extreme. It should be more likely that we would get a
result that is close to $30,000 or $40,000.
Sampling
Distribution
So, in this example it is more likely we will get sample means that are
somewhere around $37,000. If we took a large number of samples of 10 employees
and calculated the average for each, there should be a large number of sample
averages around 37,000, but we would also get a few weird ones that are far
from that number. Now, if we were to take these sample averages and plot them
in a frequency diagram, it might look something like this:
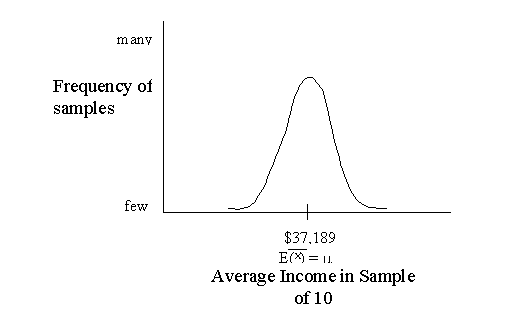
In the above figure, most of the
samples are around the middle. The middle value, which is called the expected
value of the mean (represented by E() ),
is equal to the mean of all the sample means (i.e., take the mean of each
sample and then take the mean of all those means). It just so happens that the
expected mean is equal to the population mean. That is, if we collected an
infinite number of samples and calculated the mean of each, and then calculated
the mean of all those sample means, it would equal the mean of the entire
population.
The figure above represents the sampling
distribution of the mean. The sampling distribution is like other distributions
because it has a mean (which is called the expected mean) and a standard
deviation (called the standard error). Because we calculated the mean in
each sample, the standard error is called the standard error of the mean.
We could have calculated other statistics in each sample, like the median or
the standard deviation, in which case we would have the standard error of the
median or the standard error of the standard deviation. (It turns out that
neither of the latter are used very often). Every statistic has a sampling
distribution though. A statistic is unbiased if it's sampling
distribution mean is equal to the population mean. The sample mean, , is unbiased.
This all probably sounds pretty
hypothetical (and hopefully familiar), but it is the basis of all of
inferential statistics. Inferential statistics, statistical tests, and
statistical significance are all based on guesses about sampling variability.
If we know about how the mean fluctuates from sample to sample due to chance,
we can use that information to make inferences about the population.