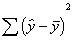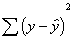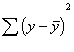lectur18

Lecture 18
R² and Tests of Significance

The Relationship Between r and b
Correlation and regression are similar. Regression concerns the prediction of y from x. Correlation concerns the association of x and y. Note that with correlation, it does not matter which variable is x and which is y. With regression, however, we are more concerned with x as a predictor and y as an outcome (sometimes called "criterion" variable). Thus, with regression analysis, we need to determine which variable is the independent variable and which variable is the dependent variable. The x variable is the hypothesized cause, and y is the hypothesized consequence. Of course, just as with correlation, a predictive relationship does not mean that x causes y. We need a well controlled study to determine that; and if we are not able to rule out alternative explanations for the relationship (e.g., a third variable), we cannot assume a causal relationship. However, regression analysis does require that one variable is specified as a predictor of another.

We can compute b from the correlation coefficient with a little help from our friend, standard deviation:

and we could go back the other way:

R²
There is another way in which regression and correlation are related. In the previous lecture, I discussed the variation that is explained and unexplained by the regression equation. We can think of this as similar to the overlapping Venn diagrams for correlation. The amount of variation explained by the regression line in regression analysis is equal to the amount of shared variation between the X and Y variables in correlation.

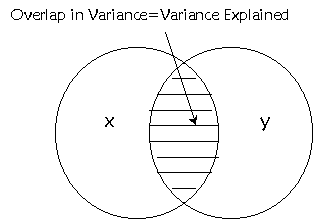
So that means we can create a ratio of the amount of variance explained (sum or squares regression, or SSR) relative to the overall variation of the y variable (sum of squares total, or SST) which will give us r-square.

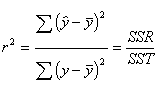
In regression analysis, r² is usually printed as R² because later we will add more predictors (independent variables) and a capital letter is used to indicate we are dealing with something bigger. For now, r²is identical to R².

F-test of R²
Just as with correlation, we may want to see if the value of r is significantly different from zero, so we could use the same t-test we used before. Usually, in practice, researchers (and computers) tend to use the F-test for testing the significance of r-square rather than the t-test for correlations when conducting regression analysis. Because we know that the t-test and the F-test are related, we are dealing with equivalent tests.

In order to create an F-test, we need to have a ratio of variances. Any idea what those variances might be?? You guessed it (at least I hoped you guessed it). To create an F-test we will use these same variances, the variance explained (SSR), the variance unexplained, and the sum of squares total (SST). We first need to obtain the mean square before the F. To do that, we just need to know what the d.f. will be for dividing the Sum of Squares values (and our instructor always gives us that).

Source of Variance	Sum of Squares Abbreviation	SS Formula	Interpretation	Mean Square	F-test
Regression	SSR		Variation in the y variable explained by the regression equation. Deviation of the predicted scores from the mean. Improvement in predicting y from just using the mean of y.
Residuals (or error)	SSE		Variation in the y variable not explained by the regression equation. Deviation of y scores from the predicted y scores. Error variation.
Total	SST		Total variation in y. Deviation of y scores from the mean of y.	not used

Does this look familiar at all?? It should. It looks exactly like the ANOVA table we created!! Oh no! Not again!! Yes, again. Regression and ANOVA are the same.

Imagine a predictor X that is dichotomous and a criterion variable (dependent) that is continuous. In this case, ANOVA and regression analysis are equal. Technically speaking, the equivalence depends on a couple of details--how you decide to code the dichotomous predictor and if the two groups are of equal size. But the bottom line is that ANOVA is a special case of regression analysis, because under certain conditions, they are equal. Regression analysis is more general, however, because it is not limited to independent variables that are dichotomous.

t-test of b
Sometimes we wish to test the slope, b, in the regression equation for significance. Although b and r are not exactly equal, their tests are equivalent. If we have test r, we don't really need to test b. However, a little later on, we will want to test them separately. You should arrive at the same t-test value for both.

When we test b for significance, we are testing the null hypothesis that in the population, the slope is 0. The population slope is represented by the Greek letter for b, b (or "beta"). So, our statistical hypotheses are this.

Below are the equations for testing b for significance. As usual, we need an estimate of the standard error of our statistic b to get to the t-test.

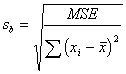
In the above equations, s_b is the standard error of b, representing the estimate of the variability of the slope from sample to sample. MSE is the mean square error we obtained above (Daniel uses a different notatio,,for the MSE sometimes). Notice that x's are involved in the computation of the standard error of b. That is because we use x's to get an estimate of b, the slope. d.f. for this test is 1 and the usual t table is used.

Standardized b
The slope, b, is interpreted as the number of units (or points on the scale) of increase in y as a result of 1 unit of increase in x. The slope then depends on what scales we are using for x and y. If we measure fat intake with the percentage of daily recommended intake rather than the grams of fat, we would wind up with a different slope, because 1 percentage change is not the same as one gram change. Similarly, if we used some different scale of measurement for cholesterol the slope would be different. Notice that in these situations, the actual variables being measured (fat intake and cholesterol) are identical either way, it is just that they are represented by a different scale. Think about measuring height in feet and inches. They are both measures of height and they are equivalent measures, but they use different scales. Although using different scales of measurement will affect the slope value, the relationship between x and y will be the same. The correlation will be the same regardless of which scaling you use. This creates a problem, because the slope value is not that informative sometimes. We need a standardized measure of the slope, just like the standardized measure of association, correlation.

I will call the standardized version of b, "B". Some texts and the output in SPSS called the standardized version "beta." Beta is also used as the population version of the unstandardized slope. So, this all gets quite confusing. Here is the formula to find the standardized version of the slope, B (and the one for getting back):

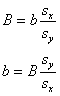
My guess is that this formula looks awfully familiar to you. Yes, it's true: the standardized slope is equal to the correlation coefficient. (note that this only applies when there is one predictor, which I will return to later).

To b or not to b
SPSS will print two slopes, one standardized and one unstandardized. Often, they are referred to as regression "coefficients" on the printout. Researchers have to make a choice about which they should report or examine. The significance test of the slope applies to both the standardized and the unstandardized, and indicates that there is a relationship between them.

The standardized B can be interpreted like a correlation coefficient. It's possible values range from -1.0 to +1.0, with zero indicating no relationship. The advantage to the standardized B is that it is scale free. A slope of .6 between two variables is the same as .6 between two completely different variables. The disadvantage is that, under some circumstances, it does not provide very good information about particular predicted values. For instance, in our fat intake example, we might want to know exactly how much the cholesterol will be reduced if we reduce the fat intake each day by 30 grams. For this type of question, the standardized B is of no assistance. However, in many other situations, the measures used do not have very meaningful scaling (e.g., a Likert-type questionnaire), and the unstandardized coefficient does not provide very useful information. This is why most social scientists tend to report the standardized coefficients. Researchers in biology and physics will often report unstandardized coefficients, because they are interested in the particular scale values. Health researchers may use either, depending on the context and the specific researcher's preferences.

A Comment on the Intercept
The intercept in regression analysis is not used very often. It represents the value of y when x equals zero, and it does not have a standardized version. It is tested for significance on the printouts, but usually the test does not make much sense. The significance test of the intercept coefficient is just the test of whether it is significantly different from zero. Most of the time this is not very meaningful and researchers usually do not even report it in articles. There are some conditions under which the intercept might be useful, but this usually applies to situations in which the values of x have a meaningful zero point (e.g., x is a ratio scale). In these cases, it might be useful to know what value of y is predicted when x is zero.