Lecture 11
Chi-square
Chi-square (or X2 after
the Greek letter for c) is a widely used statistical test which is officially
known as the Pearson chi-square in homage to its inventor, Karl Pearson.
One reason it is widely used is that it can help answer a number of different
types of analytic questions. Daniel discusses a several of these different
uses. Despite all of these potential uses, probably 90% of all uses of
chi-square involve analysis of contingency tables covered on pp. 595-598. A 2 X
2 contingency table is a table that presents counts of participants in each of
four cells. The four cells are formed by two dichotomous variables. The
contingency table analysis is the only chi-square test that we will calculate
in this class, but it is important for you to understand the other uses of
chi-square. So, I'll devote this lecture to contingency table analysis and then
mention some of the other chi-square uses.
Chi-square can be thought of in
several ways. The first way we can think of the chi-square test is as an
analogy to the t-test in which we are interested in comparing two groups. Only
chi-square is used instead, because the dependent variable is dichotomous. So,
a 2 X 2 ("two-by-two") chi-square is used when there are two levels
of the independent variable and two levels of the dependent variable. This
might be called a test of homegeneity because we are testing whether two
groups are the same. Homegeneous means "same type."
Another way to think of the same
test is as a goodness-of-fit test. The goodness-of-fit test concerns
frequencies of participants in a sample, and whether or not those frequencies
are the frequency we would expect due to chance. For instance, the frequencies
might involve how many participants said "no" and "yes" in
response to a survey question. Imagine a survey question in English that was
posed to an immigrant population that did not understand English well. If the
respondents to the survey did not understand the question asked, frequency of
no and yes responses might be a matter of chance. The goodness-of-fit analytic
question then concerns whether or not the survey respondents said yes or no
with a frequency that we would expect due to chance or not. If the respondents
did not understand the question, we would expect about 50% to answer yes and
50% to answer no. The goodness-of-fit, then concerns whether the actual
frequency of yes/no responses matches the frequency we would expect due to
chance.
Now, it turns out that the question
of homogeneity (group differences) and question of goodness-of-fit are really
the same question. If we ask whether two groups (say males and females) are
equal in their tendency to say yes to a survey question, we are also asking
whether the rate at which each group responds yes and no is the rate we would
expect from chance. Thus, the computation of chi-square concerns the match
between the expected frequencies, based on the overall number of people in each
group, and the obtained frequencies.
Chi-square can also be thought of as
a test of whether two variables are independent or not, and, thus, it is
considered a test of independence. An independence question might
concern whether gender (male vs. female) is related to responses to a yes/no
question of a survey. If gender is related to saying yes to the question, the
two variables are not independent of one another--they are dependent or
related.
So, researchers use chi-square to
answer questions about homogeneity, goodness-of-fit, or independence. If you
think hard enough about these three questions, they all turn about to be the
same question! Heavy, huh?!
Contingency tables
(2 X 2)
The contingency table is just a summary table of the data. Let's take an
example of a typical use of chi-square that compares two groups on some
dichotmous measure. Let's say we accessed some local data on voter registration
to see if males and females were equally likely to be Republican or Democrat.
We got a list of 180 voters and entered their political affiliation into a
database. To do that we just need two variables (other than an ID
variable)--gender and political affiliation. We would enter that data in the
normal way (using codes 0 and 1 to indicate male and female etc.), but, for
convenience, we (or a computer) would summarize that information in a table
like this:
|
|
Females |
Males |
Total |
|
Democrats |
50 |
70 |
120 |
|
Republicans |
19 |
41 |
60 |
|
Total |
69 |
111 |
180 |
There are 180 cases total, with 120
Democrats, 60 Republicans, 69 females, and 111 males. Overall, there are more
males than females, so to know if males or females are more likely to be
Democrat or Republican, we need to take into account the total number of each.
Because there are more males, we expect there to be a higher frequency of males
in both the Republican and Democratic groups. So, we need to take those base
rates into account to figure out the frequencies we would expect due to chance.
The formula for computing chi-square
is a matter of gauging how closely our observed frequencies in each cell of the
table are matched to the expected frequencies.
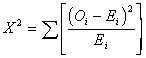
In the table Oi stands
for the observed frequency in one cell and Ei stands for the
expected frequency of that cell. As you can see in the formula, we compute
chi-square by summing up the differences between the observed and the expected
frequency for each cell.
When we do not have any information
about the expected frequency in each cell, we can compute it based on the total
number of males and females or yes and no responses. As long as we are testing
the notion that the cells are equal or not in their expected rate, we can use
the following handy-dandy computation formula instead of going through the
involved process of calculating the expected frequencies, computing the
differences, and summing them up. Here is the short hand method:
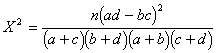
This is much easier than it looks,
because a, b, c, and d just refer to the frequency in each of the cells. n, as
usual, is the number of cases in the sample. The formula does not make too much
sense, because it is just a short cut for computing chi-square when we have a 2
X 2 contingency table.
|
|
Females |
Males |
|
Democrats |
a |
b |
|
Republicans |
c |
d |
We just do some muliplying, adding,
subtracting, and squaring and, presto, a chi-square. Here we go:
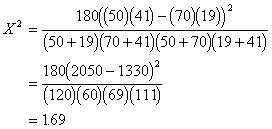
To see if this descrepancy between
observed and expected is likely to be due to sampling error, we test the
calculated chi-square for significance. The d.f. is equal to (r - 1)(c - 1) =
(2 - 1)(2 - 1) = 1, where are r is the number of rows and c is the number of
columns. We look up in Table F in the back of the book under the .95 column
(for alpha = .05). The critical value in the table is 
, and we conclude that there are
no significant differences between males and females in their political
affiliations.
More than 2
categories
Chi-square can also be used with more than two categories. For instance, we
might examine gender and political affiliation with 3 categories for political
affiliation (Democrat, Republican, and Independent) or 4 categories
(Democratic, Republican, Independent, and Green Party). In that case we can't
use our handy-dandy formula for 2 X 2 tables, but we can use a computer!
Because chi-square can be thought of as a test of goodness-of-fit, it doesn't
really matter whether we think of gender or political affiliation as the
independent variable. The test will be the same either way. Chi-square then
applies to situations where we have 2 X 3 or 3 X 4 or 5 X 6 tables. When there
is more than a 2 X 2 table, we have an omnibus test, because the test just
indicates if there is any differences among the cells. To look for specific
cell differences, researchers usually analyze separate subtables of 2 X 2s or
another method called loglinear analysis (which we won't cover in the class).
Other measures of
fit
You will also see some
alternatives to Pearson chi-square. Two, in particular, are the likelihood
ratio test (G2) and the Neyman weighted least squares chi-square
(Q). We will discuss the likelihood ratio test more later, and the Neyman test
is not used very often. All three are very similar, especially with a large
sample size.
Yate's Correction
and Fisher's Exact Test
You will often see two other statistics printed out by statistical packages.
Yate's continuity correction is a correction of Pearson chi-square that adjusts
the chi-square for smaller samples. The reason for the correction is that the
sample is based on dichotomous data, and critical chi-square values are based
on a continuous distribution. Incidentally,
or 
, so chi-square is a function of the normal
distribution (remember the end of the lecture on the binomial distribution?).
Yates correction is usually a conservative estimate of chi-square, because the
value of chi-square is adjusted downward. There is considerable disagreement
about whether or not Yate's correction is too conservative or not, and judging
from most stats texts I've seen, I think most statisticians prefer not to use
it.
The Fisher's exact test is used when
there are unequal numbers in the groups, and the accuracy of the test is a
concern, because there are very low expected frequencies in the cells. Fisher's
exact test adjusts chi-square for this problem. Usually, Pearson chi-square is
ok if there is an expected frequency of 5 or more in 80% of the cells, and an
expected frequency of 1 or more in the remaining 20% of cells. Computer
packages usually print a warning when these expected frequencies are low. When
this warning occurs, many researchers like to examine the Fisher's exact test.
Non-contingency
Analysis with Chi-square
Above I mentioned that the
chi-square calculations I used were based on the assumption that by chance, we
expect that there is an equal probability of occurrence in each group. For
instance, chance of responding yes or no is 50% for each. Usually the expected
frequency is not known and must be computed from the data, and the assumption
is that there will be equal proportions (e.g., 50% for 2 groups, 33% for three
groups, and so on). Sometimes, however, the proportion expected from chance is
known by the researcher or there is some reason to expect what the distribution
will be like. In this case, the Poisson distribution or another distribution
can be used to compute the expected frequencies. These other situations are
discussed more completely by Daniel. I think you should review them and
understand when they are used, but, because they are seen relatively
infrequently, I do not want you to spend a lot of time on them. When you run
into these situations, the Daniel text will provide a nice reference book if
you need to figure out how to calculate these or whether your situation is
relevant.
For an example SPSS output, click here.