Some research activities



Curvature of curves, surfaces, and higher dimensional manifolds are geometric concepts that are foundational not just in mathematics, but also in fields like relativity, computer graphics, and structural shells. We are contributing to the development of practical and mathematically sound ways to compute curvature, with particular emphasis on intrinsic notions, those that rely only on information internal to the manifold. Although it might seem that a surface's twists and turns in surrounding space are essential for understanding its curvature, we have known since Gauss that intrinsic curvature can remarkably be determined without any reference to how the surface is embedded. A being, living entirely within a two-dimensional surface, can compute it using only measurements of lengths and angles (the metric) within the surface. This being's viewpoint is not unlike the human condition: we ourselves live within a four-dimensional spacetime, where curvature governs gravity, and our observations are necessarily confined to what can be measured from within our spacetime. Building on this intrinsic viewpoint, our work extends classical notions of Riemann curvature to piecewise smooth metrics. The need to generalize to nonsmooth metrics is not only foundational in geometry, but also essential for numerical computations. By accounting for curvature contributions arising within elements, across nonsmooth interfaces, and from angle defects, we construct a generalized Riemann curvature that depends only on a given nonsmooth metric.

Papers: [2025], [2024], [2023].



Our generalization of curvature to nonsmooth manifolds has distributional curvature contributions at nonsmooth interfaces. In these figures of intersecting tori, the visualized Gauss curvature includes a measure at the nonsmooth intersection.






Streamlines of an exactly divergence-free velocity field around an airplane wing and tail modeled by curved elements
At the heart of all viscous incompressible flow simulators is an efficient and accurate Stokes solver. Our research yielded new finite element methods for Stokes flow, called the Mass-Conserving Stress-yielding (MCS) method. It has structure preservation properties of exact mass conservation and pressure robustness (robustness with respect to the Reynolds number). In addition the MCS method yields (without postprocessing) accurate approximations for the fluid's viscous stress, pressure, and vorticity. To approximate viscous stresses, we developed new tensor-valued finite elements with continuous shear (normal-tangential) components. MCS discretization is now often used within Navier-Stokes flow solvers and have proven particularly attractive for high-fidelity flow simulations with stress boundary conditions.

Papers: [2023], [2020], [2019].






Microstructured optical fibers such as photonic bandgap fibers and antiresonant fibers show great potential for low-loss light flow. They guide energy in leaky modes, also known as quasi-normal modes or resonances. Even though accuracy in computation of confinement losses of leaky modes is of considerable practical importance, it is often hard-won. We have approached this computation using a frequency-dependent perfectly matched layer (PML) and high order finite element discretizations. The discretization results in a polynomial eigenproblem. Our techniques have uncovered surprising variability in confinement losses with respect to modeling approaches and geometrical parameters. We have developed automatic self-adaptive algorithms that allocate degrees of freedom where needed most to capture fine scale modal features and confinement losses accurately.

Papers: [2025], [2023], [2022].



Leaky mode of an antiresonant fiber (with a hollow core of ≈15 µm)





 
Tents being built on a spatial domain (time direction is vertical)

An off-the-beaten-track idea for designing numerical schemes for hyperbolic systems is to use causality when subdividing the spacetime. In tent-shaped subregions of the spacetime, causality can be guaranteed easily by constraining the height of the tent pole. We then stratify a spacetime simulation region in an unstructured manner, by tent-shaped subregions, as shown aside. Methods built on such tents advance hyperbolic solutions asynchronously across unstructured layers. The partitioning into tents provides a rational design for local time stepping, maintaining high order accuracy in both space and time, and without any ad hoc projection or extrapolation steps. Notice how time step variability is automatically achieved in regions where large and small structures meet in the figure aside.


Accessible tutorial: [github.io/ngstents]
Papers: [2022], [2021], [2020]
Code: [github.ngstents]





High-power lasers are enabling some of the grand scientific experiments of our time (such as LIGO and NIF), not to mention their obvious demands in telecommunications and defense. Currently, one of the major impediments to scaling up power in optical laser fiber amplifiers is a phenomena called transverse mode instability or just TMI.





The above result, produced using our unique simulation tools shows how a laser beam's spatial coherence is lost due to TMI (right). The simulation shows how the coherence loss is correlated to the unwanted exchange of powers (left) between different transverse modes of the fiber. This result is obtained using the model of a thulium-doped fiber amplifier described in the paper linked here.




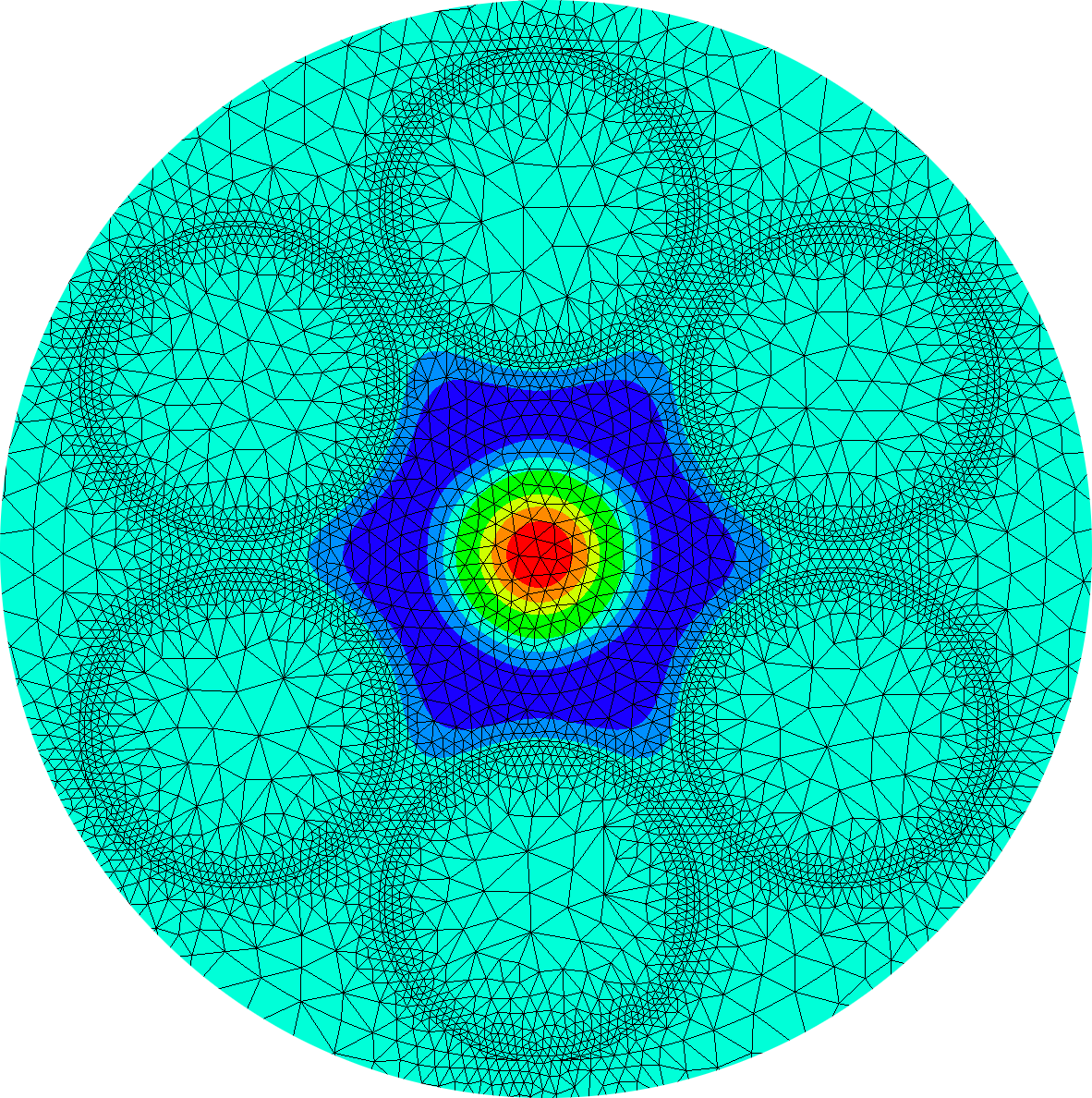
Bound states in a Schrödinger potential well
Eigenfunctions of differential operators are important in many fields. The picture aside shows plots of five computed eigenfunctions that are well localized within a potential well (which is also shown overlaid). Such targeted eigenspaces and accociated eigenvalue clusters can be approximated by a filtered subspace iteration, popularly known as the FEAST algorithm. Departing from the usual approach of analyzing such algorithms on discretized eigensystems, we studied how errors due to the approximation of the differential operator propagates through the algorithm. We also offer public domain codes containing python classes for experimenting with such algorithms.





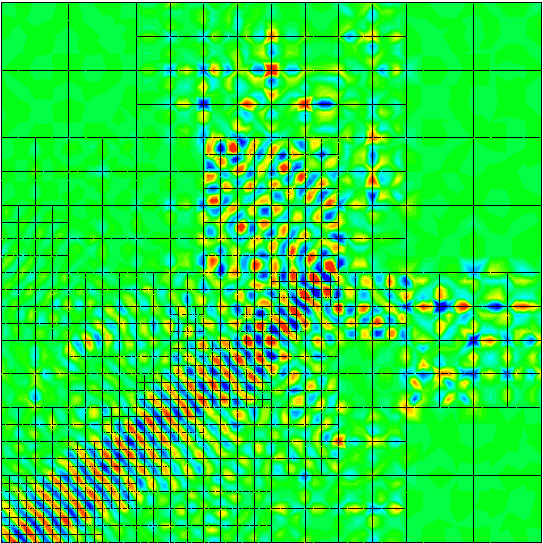
Discontinuous Petrov Galerkin (DPG) schemes provide self-adaptive residual minimizing techniques. They have a built-in error estimator which can be used to drive mesh adaptivity even for complicated differential equations. The figures aside show how a directional wave is correctly captured by an adaptive DPG scheme, while an adaptive algorithm using the standard finite element method meanders when deciding where to refine. The preasymptotic stability (in addition to the usual asymptotic stability) of DPG methods have made them a popular choice in adaptive simulations. The DPG methodology was designed using novel combinations of "broken" Sobolev spaces and interface variables.

Acta Numerica Review: [2025].

DPG
FEM
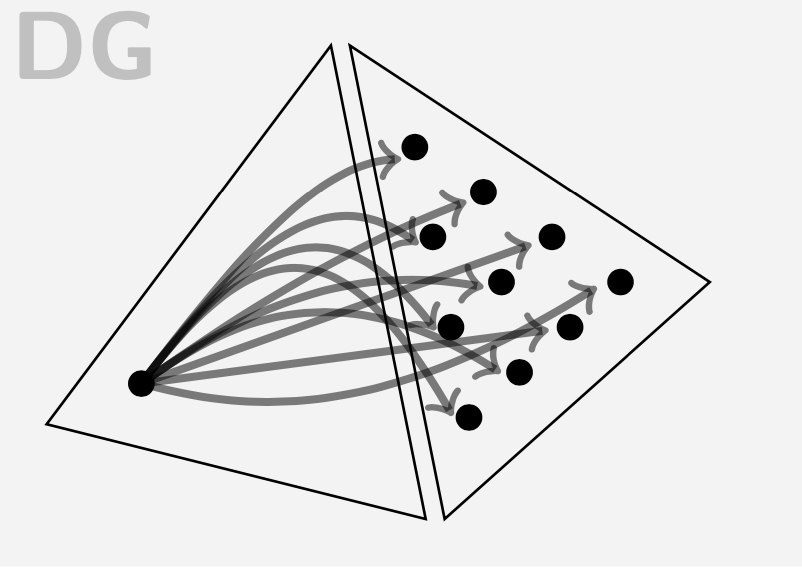
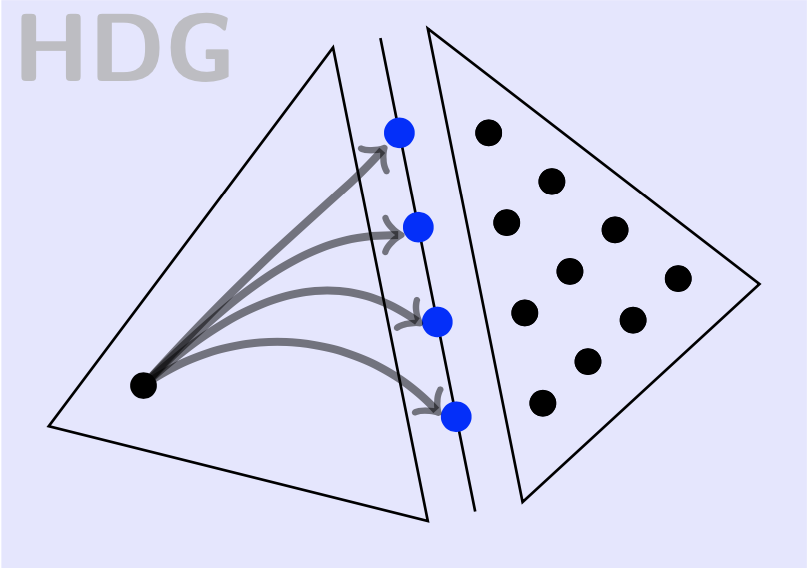
Hybridization, in the finite element context, is the process of formulating methods exploiting unknowns at the interfaces of mesh elements. Our research unearthed the popular Hybridizable Discontinuous Galerkin (HDG) methods, first introduced in our widely read paper.

The essential difference in the design of a traditional discontinuous Galerkin (DG) method and an HDG method is pictorially illustrated aside. In traditional DG, a finite element node typically interacts with all nodes of an adjacent element. In contrast, in the HDG method it interacts only with interfacial nodes. This allows the elimination (or condensation) of all unknowns except the interfacial nodes, thus overcoming an old criticism that DG methods have too many unknowns. HDG's flexible and transparent stabilization mechanism, via an unconstrained stabilization parameter, enabled many researchers to extend the HDG method to a wide variety of equations.