F(z,β) = ε
F(z,β) defines the functional form of the model, where z = [y x] is the data matrix which includes both dependent (endogenous) y and independent (exogenous) x variables, β is the vector of unknown parameters and ε is the model error. A typical nonlinear model in econometrics takes a separable form (between y and x) like this:
ε = F(z,β) = F(y,x,β) = y - f(x,β), or
y = f(x,β) + ε
For a general nonseparable (between y and x) nonlinear model F(z,β), the asymptotic theory of nonlinear least squares does not apply. Maximum likelihood or generalized method of moments should be considered instead.
S(β|y,x) = ε'ε = (y-f(x,β))' (y-f(x,β))
Least squares estimates of the parameters are computed from the first-order condition for minimization (zero gradient):
∂S/∂β = 2ε'(∂ε/∂β) = - 2ε'(∂f(x,β)/∂β) = 0.
Finally, the following Hessian matrix must be checked for the positive definiteness:
| ∂2S/∂β∂β' | = 2[(∂ε/∂β)'(∂ε/∂β) + ∑i=1,2,...,Nεi (∂2εi/∂β'∂β)] |
| = 2[(∂f(x,β)/∂β)'(∂f(x,β)/∂β) - ∑i=1,2,...,Nεi (∂2f(xi,β)/∂β'∂β)] |
Given E(∂S/∂β) = 0, following from Taylor approximation of ∂S/∂β at the NLS estimator b of β, the asymptotic theory implies that
√N(b-β) →d N(0,H-1VH-1)
where V = Var(∂S/∂β) = E((∂S/∂β)'(∂S/∂β)), and H = E(∂2S/∂β∂β').
Evaluated at the NLS estimator b of β, the sample analogy of H and V is respectively:
H = 2[(∂ε/∂β)'(∂ε/∂β)]/N
V = 4[(∂ε/∂β)'εε'(∂ε/∂β)]/N.
Therefore, b ~a N(β,[(∂ε/∂β)'(∂ε/∂β)]-1 [(∂ε/∂β)'εε'(∂ε/∂β)] [(∂ε/∂β)'(∂ε/∂β)]-1)
Under the assumption of homschedasticity, E(εε') = σ2I, the estimated variance-covariance matrix of the parameters b is simplified as follows:
Var(b) = s2[(∂ε/∂β)'(∂ε/∂β)]-1
where s2 is the estimated model variance σ2. That is, s2 = e'e/N, and e = y-f(x,b) is the estimated errors or residuals.
If there are equality or inequality parameter constraints (e.g., non-negativity) expressed in terms of a continuous transformation β = φ(α) where α is an unconstrained parameter vector. Then from the estimator of α and Var(α), we have
β = φ(α)
Var(β) =
(∂φ/∂α)
[Var(α)]
(∂φ/∂α)'
S*(β|y,x) = ε*'ε*
Since the weighting function w may depend on the unknown parameters β, the consistency condition is not satisfied in general for the weighted least squares model. Weighted least squares estimator may be inconsistent.
ll(β,σ2|yi,xi) = -½ [ln(2π)+ln(σ2) + εi2/σ2] + ln(Ji(β))
where εi = F(yi,xi,β), and Ji(β) = |∂εi/∂yi| is the Jacobian of transformation from εi to yi. The model is estimated by maximizing the sum of log-likelihood over a sample of N observations as follows:
ll(β,σ2|y,x) = -½N [ln(2π)+ln(σ2)] -½ (ε'ε/σ2) + ∑i=1,2,...,Nln(Ji(β))
The solution is obtained from the system of first-order condition as follows:
∂ll/∂β =
- ε'/σ2
(∂ε/∂β)
+ ∑i=1,2,...,N[1/Ji(β)](∂Ji/∂β) = 0.
∂ll/∂σ2 =
- N/(2σ2)
- ε'ε/(2σ4) = 0.
Usually the maximum likelihood estimation is performed by substituting out the asymptotic variance estimate σ2. That is, σ2 = ε'ε/N. Then the following concentrated log-likelihood function is maximized to find the parameter estimates β:
ll*(β|y,x) = -½N [1+ln(2π)-ln(N)] -½N ln(ε'ε) + ∑i=1,2,...,Nln(Ji(β))
Let ε* = ε/[(J1...JN)1/N]. Then the last two terms of the above concentrated log-likelihood function can be combined and the function is re-written as
ll*(β|y,x) = -½N [1+ln(2π)-ln(N)] -½N ln(ε*'ε*)
Therefore, maximizing the concentrated log-likelihood function ll*(β|y,x) is equivalent to minimizing the sum of squared weighted errors:
S*(β|y,x) = ε*'ε*
where ε* = wε, with the weight w = 1/[(J1...JN)1/N] (inverse of the geometric mean of Jacobians) applied to each observation of the error terms ε.
Solving from the first-order condition or zero-gradient condition:
∂ll*/∂β = -½N ∂ln(S*)/∂β = -½(N/S*)(∂S*/∂β) = -(N/S*)[ε*'(∂ε*/∂β)] = 0,
the solution must be checked for the negative definiteness of the Hessian matrix (the second-order condition):
| ∂2ll*/∂β∂β' | = ½N ∂2ln(S*)/∂β∂β' |
| = ½(N/S*)[(1/S*)(∂S*/∂β)'(∂S*/∂β) -(∂2S*/∂β∂β')] |
Since ∂S*/∂β = 0 from the first-order condition for the maximum likelihood solution, the corresponding negative definite Hessian matrix is simply
| ∂2ll*/∂β∂β' | = -(N/S*)[½(∂2S*/∂β∂β')] |
| = -(N/S*)[(∂ε*/∂β)'(∂ε*/∂β) + ∑i=1,2,...,Nεi* (∂2εi*/∂β∂β')] |
Given E(∂ll*/∂β) = 0, following from Taylor approximation of ∂ll*/∂β at the ML estimator b of β, the asymptotic theory implies that
√N(b-β) →d N(0,H-1VH-1)
where V = Var(∂ll*/∂β) = E((∂ll*/∂β)'(∂ll*/∂β)), and H = E(∂2ll*/∂β∂β').
Evaluated at the ML estimator b of β, the sample analogy of H and V is respectively:
H = (-1/σ2*)[(∂ε*/∂β)'(∂ε*/∂β)]/N
V = (-1/σ2*)2[(∂ε*/∂β)'ε*ε*'(∂ε*/∂β)]/N,
where σ2* = S2/N.
For a class of models satisfying regularity assumptions, the Information Matrix Equality holds as - H = V or
- E(∂2ll*/∂β∂β') = E((∂ll*/∂β)'(∂ll*/∂β))
Therefore, √N(b-β) →d N(0,-H-1). In other words, b ~a N(β,σ2*[(∂ε*/∂β)'(∂ε*/∂β)]-1)
The estimated variance-covariance matrix of the parameters b is:
Var(b) = s2*[(∂ε*/∂β)'(∂ε*/∂β)]-1, where s2* is the sample estimate of σ2*.
Further, as in the case of nonlinear least squares, if there are equality or inequality parameter constraints (e.g., non-negativity) expressed in terms of a continuous transformation β = φ(α) where α is an unconstrained parameter vector. Then from the estimator of α and Var(α), we have
β = φ(α)
Var(β) =
(∂φ/∂α)
[Var(α)]
(∂φ/∂α)'
ll*(β|y,x) = -½N [1+ln(2π)-ln(N)] -½N ln(ε'ε)
This is exactly the special case of classical nonlinear model in which ε = F(y,x,β) = y - f(x,β). For this special case, maximizing the concentrated log-likelihood function ll*(β|y,x) is the same as minimizing the sum of squared errors S(β|y,x).
First, we fit the following two classical production functions based on 30 data observations of labor L, capital K, and output Q given in the file JUDGE.TXT (The data of this example is taken from Judge, et. al. [1988], Chapter 12, p. 512):
Based on the least squares and maximum likelihood criteria, estimate and compare the Cobb-Douglas and CES production function, respectively.
According to Zellner and Revankar [1970], the classical production functions may be generalized to consider variable rate of returns to scale as follows:
Modify and estimate the Generalized version of Cobb-Doulass and CES production function, repectively.
ε = F(y,x,β) ~ normal(0,σ2I).
Thus the estimated least squares or maximum likelihood parameters b of β is normally distributed:
b ~ normal(β,Var(b))
where the estimated variance-covariance matrix is
| Var(b) | = [-E(∂2ll(b)/∂β∂β')]-1 = s2[½ E(∂2S(b)/∂β∂β')]-1 |
| = s2[(∂ε(b)/∂β)'(∂ε(b)/∂β)]-1 |
and the estimated asymptotic variance of the model is s2 = S(b)/N.
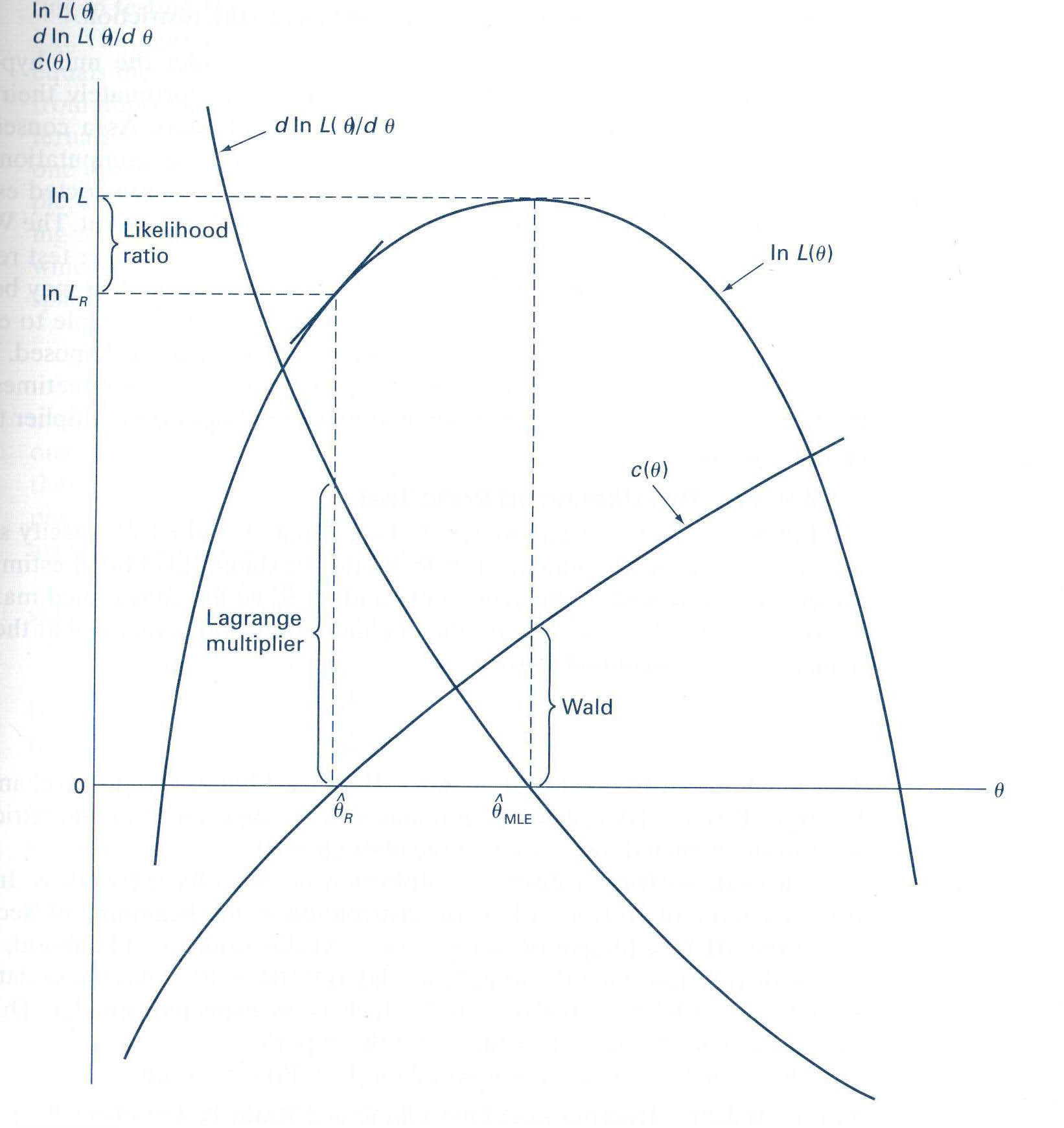
Confidence location of the true parameter vector β is derived from the estimated b based on the following familiar F statistic:
F = (S(β)-S(b))/J/s2
where J is the degrees of freedom associated with the testing hypotheses.
By approximating the sum of squares function S(β) at b up to the second order and set ∂S(b)/∂β = 0,
S(β) - S(b) = ½ (β-b)' [∂2S(b)/∂β∂β'] (β-b)
Therefore, the test statistic for testing β = b:
JF = (β-b)' [Var(b)]-1 (β-b)
follows a Chi-Square distribution with J degrees of freedom.
c(β) = 0.
If the constraints were true, without estimating the constrained model, the unconstrained parameter estimator b is expected to satisfy the constraint equation closely. That is, c(b) = 0. The test statistic
W = c(b)'[Var(c(b)]-1c(b)
has a Chi-square distribution with J degrees of freedom. With the first-order linear approximation of the constraint function c(β) at b,
W = c(b)' {(∂c(b)/∂β) [Var(b)] (∂c(b)/∂β)'}-1 c(b)
Note that this test statistic does not require the computation of the constrained parameter estimator.
The test statistic is written as:
| LM | = (∂ll(b*)/∂β) [Var(∂ll(b*)/∂β]-1 (∂ll(b*)/∂β)' |
| = (∂ll(b*)/∂β) [Var(b*)] (∂ll(b*)/∂β)' |
The estimated variance-covariance matrix of the constrained estimator b* is computed as follows:
Var(b*) = H-1 [I - G'(G H-1G')-1GH-1]
where H = [-∂ll(b*)2/∂β∂β'] and G = [∂c(b*)/∂β].
LM test statistic is easily approximated with the following formula:
LM = {[ε(b*)'(∂ε(b*)/∂β)] [(∂ε(b*)/∂β)'(∂ε(b*)/∂β)]-1 [ε(b*)'(∂ε(b*)/∂β)]'}/(ε(b*)'ε(b*)/N)
Note that the maximum likelihood estimates of errors ε(b*) may be properly weighted, and this test statistic is based on the constrained parameters alone.
LR = -2(ll(b*)-ll(b))
follows a Chi-square distribution with J degrees of freedom, in which there are J constraints in the equation c(β) = 0. In terms of sum of squares, it is
LR = N ln(S(b*)/S(b)).
ln(Q) + θ Q = β1 + β4ln(β2Lβ3 + (1-β2)Kβ3) + ε
Using Wald test, Largrangian multiplier test, and likelihood ratio test to verify the nonlinear equality constraints (or classical CES): β4 = 1/β3, and θ = 0.