Lecture
4
Sample Size
In this cyberlecture, I'd like to
outline a few of the important concepts relating to sample size. Generally,
larger samples are good, and this is the case for a number of reasons. So, I'm
going to try to show this in several different ways.
Bigger is Better
1. The first reason to understand why a large sample size is beneficial is
simple. Larger samples more closely approximate the population. Because the
primary goal of inferential statistics is to generalize from a sample to a
population, it is less of an inference if the sample size is large.
2. A second reason is kind of the
opposite. Small samples are bad. Why? If we pick a small sample, we run a
greater risk of the small sample being unusual just by chance. Choosing 5
people to represent the entire U.S., even if they are chosen completely at
random, will often result if a sample that is very unrepresentative of the
population. Imagine how easy it would be to, just by chance, select 5
Republicans and no Democrats for instance.
Let's take this point a little
further. If there is an increased probability of one small sample being
unusual, that means that if we were to draw many small samples as when a
sampling distribution is created (see the second lecture),
unusual samples are more frequent. Consequently, there is greater sampling
variability with small samples. This figure is another way to illustrate this:
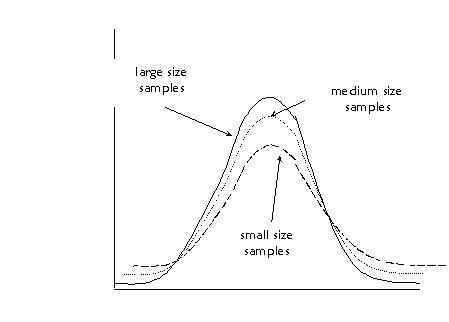
Note: this is a dramatization to illustrate the
effect of sample sizes, the curves depicted here are fictitious, in order to
protect the innocent and may or may not represent real statistical sampling
curves. A more realistic depiction can be found on p. 163.
In the curve with the "small
size samples," notice that there are fewer samples with means around the
middle value, and more samples with means out at the extremes. Both the right
and left tails of the distribution are "fatter." In the curve with
the "large size samples," notice that there are more samples with
means around the middle (and therefore closer to the population value), and
fewer with sample means at the extremes. The differences in the curves
represent differences in the standard deviation of the sampling
distribution--smaller samples tend to have larger standard errors and larger
samples tend to have smaller standard errors.
3. This point about standard errors
can be illustrated a different way. One statistical test is designed to see if
a single sample mean is different from a population mean. A version of this
test is the t-test for a single mean. The purpose of this t-test is to
see if there is a significant difference between the sample mean and the
population mean. The t-test formula looks like this:
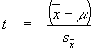
The t-test formula (also found on p.
161 of the Daniel text) has two main components. First, it takes into account
how large the difference between the sample and the population mean is by
finding the difference between them (
). When the sample mean is far from the
population mean, the difference will be large. Second, t-test formula divides
this quantity by the standard error (symbolized by 
). By dividing by the standard
error, we are taking into account sampling variability. Only if the difference
between the sample and population means is large relative to the amount of sampling
variability will we consider the difference to be "statistically
significant". When sampling variability is high (i.e., the standard error
is large), the difference between the sample mean and the population mean may
not seem so big.
|
Concept |
Mathematic Representation |
|
distance of the sample mean from the population mean |
|
|
representation of sampling variability |
|
|
Ratio of the distance from the population mean relative to the sampling variability |
t |
Now,
back to sample size... As we saw in the figure with the curves above, the
standard error (which represents the amount of sampling variability) is larger
when the sample size is small and smaller when the sample size is large. So,
when the sample size is small, it can be difficult to see a difference between
the sample mean and the population mean, because there is too much sampling
variability messing things up. If the sample size is large, it is easier to see
a difference between the sample mean and population mean because the sampling
variability is not obscuring the difference. (Kinda nifty how we get from an
abstract concept to a formula, huh? I took years of math, but until I took a
statistics course, I didn't realize the numbers and symbols in formulas really
signified anything).
4. Another reason why bigger is
better is that the value of the standard error is directly dependent on the
sample size. This is really the same reason given in #2 above, but I'll show it
a different way. To calculate the standard error, we divide the standard
deviation by the sample size (actually there is a square root in there).
In this equation, 
is the standard error, s
is the standard deviation, and n is the sample size. If we were to plug
in different values for n (try some hypothetical numbers if you want!), using
just one value for s, the standard error would be smaller for larger values of
n, and the standard error would be larger for smaller values of n.
5. There is a rule that someone came
up with (someone who had vastly superior brain to the population average) that
states that if sample sizes are large enough, a sampling distribution will be
normally distributed (remember that a normal distribution has special
characteristics; see p. 107 in the Daniel text; an approximately normally
distributed curve is also depicted by the large sample size curve in the figure
above). This is called the central limit theorem. If
we know that the sampling distribution is normally distributed, we can make
better inferences about the population from the sample. The sampling
distribution will be normal, given sufficient sample size, regardless of
the shape of the population distribution.
6. Finally, that last reason I can
think of right now why bigger is better is that larger sample sizes give us
more power. Remember that in the previous lecture
power was defined as the probability of retaining the alternative hypothesis
when the alternative hypothesis is actually true in the population. That is, if
we can increase our chances of correctly choosing the alternative hypothesis in
our sample, we have more power. If the sample size is large, we will have a
smaller standard error, and as described in the #3 and #4, we are more likely
to find significance with a lower standard errror.
Do I seem like I am repeating
myself? Probably. Part of the reason is that it is important to try to explain
these concepts in several different ways, but it is also because, in
statistics, everything is interrelated
How Big Should My
Sample Be?
This is a good question to ask, and it is frequently asked. Unfortunately,
there is not a really simple answer. It depends on the type of statistical test
one is conducting. It also depends on how precise your measures are and how
well designed your study is. So, it just depends. I often hear a general
recommendation that there be about 15 or more participants in each group when
conducting a t-test or ANOVA. Don't worry, we'll return to this question later.