lecture3

Lecture 3
Significance Testing

The Purpose and Meaning of Significance Testing
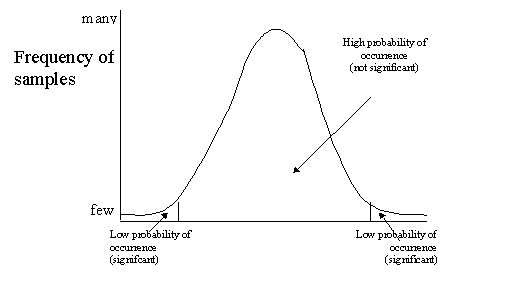
When discussing sampling variability, I stated that the whole purpose of doing statistics was to take into account sampling variability. I didn't lie. When we conduct a test to see if a sample statistic is statistically significant, we are checking to see if the sample statistic is an anomaly or not. Is that statistic for the sample different from the one in the population merely because of chance factors, or the difference big enough that we would consider it important? If we want to check the likelihood that the sample of 10 participants we have chosen to survey about their annual income have incomes that are different from the Portland metropolitan average, we would conduct a significance test. Now, almost every sample we would draw would have an average income that was different from the Portland average, but most of the samples should be very close to the Portland average. So, there is a high probability that the sample will be close to the population value and a very low probability that it will be far from it. If we find a sample value that is extreme and there seems to be a very low probability of it's occurrence, then we consider it significant. We're making a guess that this extreme value has a very low probability that it is so high or so low just because of sampling variability.

The income example is one that I chose because it was simple. In actual practice, this type of statistical question (or hypothesis) is not asked very often. Usually we don't have information about the population. In fact, during this course we'll be dealing only with statistical tests that ask more complicated questions than this one. So let's detour a moment and talk about statistical hypotheses.

Statistical Hypotheses
All experiments and other studies test specific hypotheses. Most statistics texts will tell you that in conducting any statistical test there are two hypotheses being considered. The hypothesis that the researcher is really interested in is called the alternative (or sometimes the "experimental") hypothesis (or H₁), and the other is called the null hypothesis (or H₀). The null hypothesis is a kind of "strawman"; it's a hypothesis that we want to disprove. The reason for all this is that the great scientific philosophers (like Karl Popper) argue that we cannot logically prove something to be true, we can only disprove it (we create hypotheses that are falsifiable). When we compare two group means, for instance, the null hypothesis states that they are equal to one another. The alternative then is that they are unequal, and if we wind up disproving or rejecting the null hypothesis, that is what we will conclude.

In the income example, the null hypothesis would state that the a particular sample average is not significantly different from the population value (). It is different only due to chance factors. In other words, the sample mean is not really any different from the population mean once we take into account sampling variability. If the null is not true, we accept the alternative hypothesis, that the sample mean is not equal to the population mean (). Notice that I said "accept" the alternative hypothesis. Technically, we can't prove that it is true, so we just retain it until it is proven wrong.

The alternative hypothesis must be stated in a way the predicts differences. The null hypothesis always predicts no differences. Let's use a more realistic example. Many times, researchers are interested in comparing two groups. As an example, let's say we are comparing aspirin to a new arthritis drug in a new experiment. In the experiment, we draw a sample of participants (using an excellent method of course) and we split them into two groups. The best way to split them into two groups is by using random assignment. Each participant has an equal chance of being in either group, and the only thing the led to their assignment to either group was random chance. Our statistical hypotheses would look like this:

H₀ (null hypothesis):	The aspirin and new drug groups will not differ (they are equal)
H₁ (alternative hypothesis):	The aspirin and new drug groups will differ (they are unequal)

H₀ (null hypothesis):	The aspirin and new drug groups will not differ (they are equal)
H₁ (alternative hypothesis):	The new drug group will have fewer symptoms than the aspirin group

(The Daniel text on pages 205 through 208 provide some more examples of how to state these.)

Statistical Decisions
Usually the end result of conducting a statistical test is whether our test statistic is "significant" or not. We decide whether to choose H₀ or H₁. Significance can be explained many ways: we have rejected the null hypothesis, the null hypothesis is disproved, the alternative hypothesis has been retained, there are differences, differences are just due to chance, or it is highly unlikely that the two groups are different just due to chance.

Let's look at the last statement more closely for a moment "it is highly unlikely that the two groups are different just due to chance". When we randomly assigned the two groups, there was a chance that the two groups might have a different number of arthritis symptoms just due to chance--before we even began the experiment and gave them drugs. These differences can be thought of as a type of sampling variability. Imagine for a minute that we were able to do our experiment on the entire population (say all U.S. residents with osteoarthritis) and that there are no differences between using aspirin and the new drug. We would know for certain if the new drug was not more effective, because we tested it on half of the entire population. In other words, we are assuming that the null hypothesis is true in the population (no differences between the two treatments). If we were to draw two small random samples from this population (some people who had gotten the new drug and some that had gotten the aspirin), we might get some differences between our two sample groups in the number of arthritis symptoms. So there is some possibility that differences between the groups might be due to sampling variability or chance. This would be a mistake though--it would be the rare instance in which our sample suggested big differences between the two groups when, in fact, testing the whole population would indicate there are no differences. This would be a statistical error.

Types of Statistical Errors: Making the Wrong Statistical Decision
With statistics, we are never certain. We just wager a guess. It's probability. When we guess, we may be wrong. Essentially there are two ways we can be wrong: (1) our sample can suggest that we should pick the alternative hypothesis when in the population, the null hypothesis is correct, or (2) our sample can suggest we should pick the null hypothesis when in the population the alternative hypothesis is correct. If you're on your toes, you've probably guessed there are also two ways of being correct. Let's organize this in a table.

	In population, H₀ is correct	In population, H₁ is correct
Based on sample, H₀ is retained	Correct Decision: No official name (1 - a)	Incorrect Decision: Type II Error (b)
Based on sample, H₁ is retained	Incorrect Decision: Type I Error (a)	Correct Decision: Power (1 - b)

When we retain the alternative hypothesis (H₁) in our sample and it is correct in the population, we have made a correct decision. The probability that we make a correct decision is called power. Power is good, and we want lots of power (statistical power, that is!). We want to make as many of these types of correct decisions as possible. The actual probability that we will make a correct decision of this type is not known, because we never really know what is correct in the population. When we retain the null hypothesis (H₀) and in the population the null hypothesis is correct, we have also made a correct decision. No one has made up a name for this yet.

When we retain the alternative hypothesis and in the population the null hypothesis is really true, we have made an error. We concluded, based on our sample, that there was really a difference between our groups that was not due to chance. In other words, we believe that the new arthritis drug is actually effective. The likliehood of this happening is set to a certain value, 5% (or probability of .05). This probability is called, a, the greek letter alpha, and it is arbitrarily set. It is a conventional number, chosen because 5% seems to be a reasonably small number. When I state that a is set, it is set because we do not make a decision to reject unless the likelihood our sample statistic is different from the population value is below 5%.

When we retain the null hypothesis in the sample but the alternative hypothesis in the population is actually correct, we have made another kind of error, the Type II error. The Type II error is like missing a significant finding. There really should be a difference between the new drug group and the aspirin group, but we failed to find the difference in our sample for some reason. The probability of a Type II error occuring is designated by b, the Greek letter beta. The value for b is not known, but its probability is related to the probability of power.

The probability of correctly rejecting the null hypothesis (i.e., power) is hoped to be .80 (This is also an arbitrary number proposed by a statistician named Jacob Cohen, but it is now a widely excepted number for an "acceptable" level of power). That is, we hope that 80% of the time we will make a correct decision to reject the null hypothesis (retain the alternative) when the alternative hypothesis is really true in the population. We can do various things to improve power, but we never really know what its probability is. One of things we can do to increase power (and therefore decrease Type II errors) is to increase sample size, …which is where the next lecture takes up. Click here to go there: Sample Size.