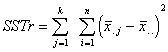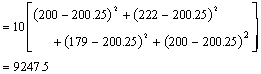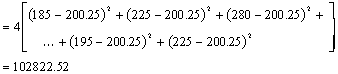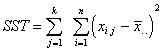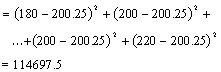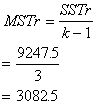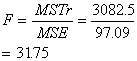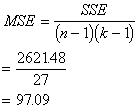Lecture
10
Within-Subjects Analysis of Variance
When to Use
Within-Subjects ANOVA
The within-subjects ANOVA is
really just an extension of the paired t-test
discussed earlier. It is used whenever there are repeated measures or repeated
treatments of an individual, paired participants (e.g., triplets), or matched
participants (e.g., four participants are yoked according to the amount of
daily exercise they get). Daniel describes two forms of the within-subjects
design, the design he calls the "randomized complete block design"
and repeated measures. The randomized complete block design is a study in
several participants are matched or yoked together (e.g., on age), then one
member of each grouping is randomly assigned to each of the treatment
conditions. If there are three treatment conditions (e.g., three different
drugs are given), each person in a group of three would be sent to a different
condition. But in order for it to be valid to use a within-subjects analysis,
the groupings of participants has to be done on some basis. For instance,
triplets or three people matched because they have the same number of years
experience on the job. Repeated measures, on the other hand, indicates that
each person is measured several times. In general, the within-subjects ANOVA
applies to matching, repeated measures, repeated treatments, or any time
participants are yoked together.
An example of a within-subjects
design would be a hypothetical study on cholesterol which has four treatments:
high oat fiber diet, exercise, a low fat diet, and low calorie diet. In a
between-subjects version of the study, different participants would be in each
of these four conditions. In a within-subjects version of this study, each
participant might be exposed to each of these treatments for a period of time.
So, if I was in the within-subjects cholesterol study (or, to be more specific,
we would call this a repeated measures design), I would spend a month eating oatmeal
for breakfast. Then, the next month, I would stop eating oatmeal, and begin an
exercise regimen. The following month, I would stop exercising, and start
reducing fat intake. And so on.
One can think of the scores on the
cholesterol measure as blocked together according to each individual. Each
person has four scores. At the end of each month (and, hence, each treatment) a
cholesterol count is taken. In a way, each participant has a block of four
scores--so you can see the similarity to the randomized block design.
Like the between-subjects ANOVA and
the between-subjects t-test, the within-subjects ANOVA and the within-subjects
t-test are related. The within-subjects ANOVA can be used for two or more
groups, and when used with two groups the t-test and the F-test will lead to
the same conclusion (
and 
).
The same benefits of the
within-subjects t-test over the between-subjects t-test still apply. We need
fewer participants overall and we have more power, because each individual (or
block) acts as its own control.
The Analysis
The analysis approach is similar to that of the paired (or within-subjects or
matched) t-test. We are intrested in the differences between scores for an
individual (remember when we calculated the difference score, d, for each
individual?). We will also use a similar ANOVA logic to the logic we used with
the between-subjects ANOVA. We will calculate the variation of the scores for
an individual relative to the mean of scores for that individual. In other
words, we want to know how much each participant's scores change from treatment
to treatment. If one or more of our cholesterol treatments had an effect, we
would expect cholesterol counts to change fairly dramatically from
month-to-month.
A Note on Notation
The notation for this analysis does not change dramatically, but we need to
extend it a little. Previously, we used a dot to indicate that we had combined
scores across individuals. For example 
referred to the sum of individual scores in
a group. This time we will do some adding the other way, so that we combine
scores across treatments rather than individuals. So, the sum of scores for one
participant in the study, summed across treatments is symbolized by 
The sum of
cholesterol counts for the second participants who has completed all four
treatment conditions would be symbolized as 
Thus, 
stands for the sum of individuals for the
second treatment, and 
stands for the some of treatments for participant 2. Similary,
represents
the mean cholesterol score for participant 2 across all treatments, and 
represents the
mean of all participants for treatment number 2.
Example
|
Participant # |
Oat Fiber |
Exercise |
Low Fat |
Low Calorie |
|
|
|
1 |
180 |
200 |
160 |
200 |
740 |
185 |
|
2 |
230 |
250 |
200 |
220 |
900 |
225 |
|
3 |
280 |
310 |
260 |
270 |
1120 |
280 |
|
4 |
180 |
200 |
160 |
200 |
740 |
185 |
|
5 |
190 |
210 |
170 |
210 |
780 |
195 |
|
6 |
140 |
160 |
120 |
110 |
530 |
132.5 |
|
7 |
270 |
300 |
250 |
260 |
1080 |
270 |
|
8 |
110 |
130 |
100 |
100 |
440 |
110 |
|
9 |
190 |
210 |
170 |
210 |
780 |
195 |
|
10 |
230 |
250 |
200 |
220 |
900 |
225 |
|
|
2000 |
2220 |
1790 |
2000 |
|
|
|
|
200 |
222 |
179 |
200 |
|
|
Now we have several sums of squares
to compute.
|
Formula |
Name |
Description |
Example |
|
|
Sum of Squares Treatment |
Represents variation due to treatment effect |
|
|
|
Sum of Squares Block |
Represents variation within an individual (within block) |
|
|
|
Sum of Squares Error |
Represents error variation |
|
|
|
Sum of Squares Total |
Represents total variation |
|
Now for the mean squares and the
computed F-value:
|
SSTr=924.75 |
k - 1=4 - 1=3 |
|
|
|
SSBl=25705.63 |
n - 1=10 - 1=9 |
not needed |
|
|
SSE=88067.12 |
(n - 1)(k - 1) =(10 - 1)(4 - 1)=27 |
|
|
|
SST=114.697.50 |
kn - 1 = 40 - 1 = 39 |
|
|
Interpretation
To check whether the calculated
F-value of 31.75 is significant, we compare that value to the critical value of
obtained
from Table G, using the table labeled .95 (for a=.05) and 3 and 27 d.f.
Our test is significant, indicating that there were differences in cholesterol
treatments that are unlikely to be due to chance. What if we had set alpha to a
lower value, say .01, would the test still be significant? To see, look up the
same d.f. values in the .99 (a = .01) table. If our calculated value
exceeds that table value, we would have significance at p <.01. Often
authors report the lowest p-value at which they would find significance (e.g.,
p < .05, p < .01, p < .001), given their calculated value. Computers
print out the exact p-value, so all one really has to do is look to see if the
p-value printed out is less than .05, .01, or .001.