The big Bang is all about understanding how the shape of spacetime changes as the Universe expands. The key to all of this is to understand how the acceleration of gravity stretches time. To see this me must first understand how fast speed stretches time. Although most folks are intimidated by just the name, Einstein’s Special Theory of Relativity is it something that any "normal" person can understand.
We begin by asking the reader to imagine riding in a streetcar as Einstein did on his way to the patent office every day. Look at the clock on the wall and note the time, say 1:00 P.M. Now suppose the streetcar you are traveling in is moving at the speed of light. As you look back at the clock, what time do you see? The light has been traveling at the speed of light for 10 minutes and you have been traveling at the speed of light for 10 minutes so the photons that left the clock face as you passed are traveling along beside you and show the clock at 1:00 P.M. If you travel for an hour, what time do you see on the clock? 1:00 P.M. If you travel for 10 hours at the speed of light, what time is it? Something is obviously funny with time because your wrist-watch shows that 10 minutes, and hour, or 10 hours have passed, yet the other clock seems frozen.
It turns out that you could never travel as fast as light, but suppose the streetcar you are traveling in is moving at the 99% of speed of light. As you look back at the clock, what time do you see? Maybe 1:01 P.M. If you travel for an hour, what time do you see on the clock? Maybe 1:38 or 1:39 P.M. We don’t know exactly how slow the wall clock is moving yet, but we know that something is still funny with time. Maybe if we look at "how slow," we will understand "why slow?"
The hard part of Special Relativity is that it forces us to abandon our ideas about time, but the basic mathematics of it are relatively simple and can be encapsulated in a simple picture. The picture depends on extending something you know about on an intuitive level. Suppose I tell you that you have an hour to drive and that you must go South at 50 Mph. Can you tell me where you will end up? Suppose I tell you to go South at 100 mph, where will you find yourself after one hour (if not in jail)? Suppose I tell you to go South for two hours at 50 mph, where do you end up? So you see, you know the distance traveled if you know how fast you are going and how much time is allowed. That is,
distance traveled is velocity multiplied by time.
Let’s check this against our intuition for the last case:
100 miles = 50 miles/hour × 2 hours
But I’m a slow typist so I want to abbreviate this understanding with the first letter of each word:
d = v t
Any heart attacks yet? Well that one relation, which you already understand on some level, is all the math you need to do basic relativity!
In 1905 Albert Einstein stated that the speed of light must be the same no matter what the state of motion is of the object that projects the beam. Now any clown walking down the street will verify that a cream pie thrown in his face by a colleague in a moving car hits his face at a much higher speed than a cream pie thrown by a clown standing near-by. Einstein said that this is not the case for clowns throwing photons of light, and no experiment has been able to disprove him. He showed that the fact that the speed of light (always represented by the letter c and measured to be 186,000 miles per second) is the same in all frames of reference had consequences that contradicted ideas of the nature of time.
Once we know the value of c, we can measure the distance to the Moon by bouncing a laser beam off it, we notice that there is a 1.28 second delay for each leg of the trip. That means that the distance between Earth and Moon is
d = c t
or
d = 186,000 miles/second × 1.28 seconds = 238,000 miles.
Consider a beam of light bouncing between the mirrors of a space ship moving (perpendicular to the beam) at velocity v relative to the ground.
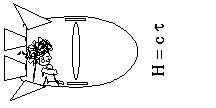
To someone sitting in the ship the distance the beam must travel is simply the height H of the ship. The distance can be measured by multiplying the velocity of light c times the time of travel t (we use the Greek symbol tau to keep the two times straight in our minds) as measured in the ship or H = c t .
Figure 1.
To someone standing on the Earth the light will be seen to follow a diagonal path because the space ship moves relative to the Earth between the time that the light is emitted near the bottom and when it is reflected from the mirror near the top of the space ship.
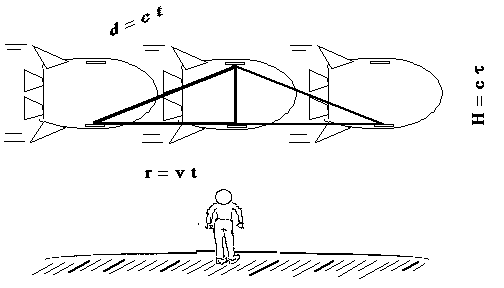
Figure 2.
Since the speed of light is the same in the Earth reference frame as in the reference frame of the ship, this diagonal distance is d = c t, where t is the time interval measured from the Earth. Finally, the ship travels a distance r = v t with respect to the Earth.
Look at Figure 2 and tell me which of lines d or H is longest. Clearly the hypotenuse d of the triangle is longer than the vertical leg H. Then since the speed of light c is the same for both the hypotenuse and the vertical leg, t must be larger than t. But the hypotenuse of any right-triangle you can draw is always longer than each leg, or is equal to the length of one leg if the length of the other is zero. (Draw several examples to prove this to yourself.) This means that t is always larger than t for nonzero v. We call this minimum time value t proper-time. It is simply the time measured in any frame of reference in which the two events are measured at the same place, such as the emission and the return points of the bouncing beam of light, or two clicks of a clock. The coordinate time interval t is measured in a frame of reference (a point of view of someone) moving at velocity v relative to another frame of reference in which the clock is stationary. (If we want to be precise, t in Figure 1 is actually half of the proper-time interval for a round trip 2t. Likewise in Figure 2, t is half of the corresponding coordinate time 2 t.)
We claimed that we could easily find the exact size of time stretch for a streetcar (or rocket) traveling past a clock tower. Suppose the rocket is traveling past the Earth at v = .9986 c. We could find how much larger t is than t by using the Pythagorean theorem and some algebra but there is a simple way to get the time dilation factor by drawing the space ship picture carefully, with v properly proportional to c:
1) Start with a square drawn on a thin sheet of paper or plastic that is 10 cm on each side (the bottom side of which represents the distance d that light travels in the coordinate frame of reference).
2) Now express the velocity of the space ship as a fraction of the speed of light and draw a rectangle whose width r is that same fraction of 10 cm wide and is the full 10 cm high. Suppose v is 
of the speed of light (111600 miles/second), then the width of the rectangle is 6 cm as in Figure 3.
3) Now rotate the square around its lower left-hand corner until the lower right-hand corner of the square just touches the right-hand edge of the rectangle.
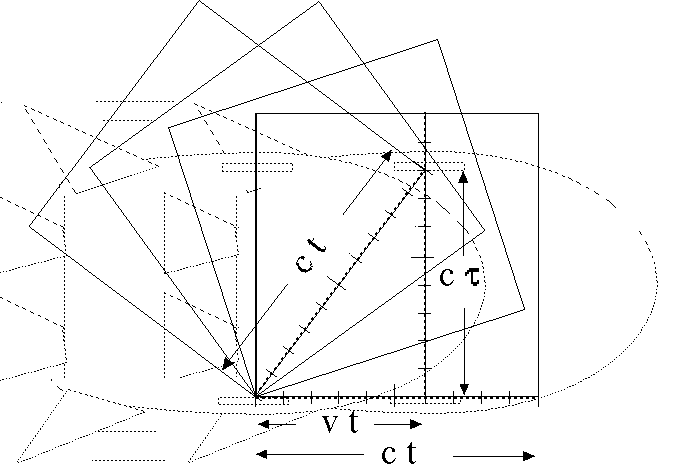
Figure 3
4) Tape the square in place and measure the distance from the lower right-hand corner of the rotated square to the lower right-hand corner of the rectangle. For the present example this length is 8 cm. Divide 10 cm by this length to get the value of the time dilation factor. In the present example this ratio is 
or 1.25 . We have sketched in ghosted images of the rocket's position when the light left the lower mirror and where it is when the light has reached the upper mirror. It helps to keep this image in your mind's eye as a reminder that we are simply doing a careful drawing of Figure 2 to get the exact amount by which coordinate time is dilated.
We could instead have used the Pythagorean theorem to give this result. Proper time in special relativity is given by
or dividing by c2 , we have
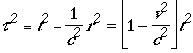(1)
You can verify that if we put in v/c = then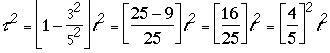 
implies that the time dilation factor t/t = .
If you stand on the Earth and watch a rocket travel past at v=0.2c, the path of light bouncing between two mirrors of the space ship traces out the diagonal path shown in Figure 5a. If the rocket were traveling past at v=0.7c, the path would be the diagonal path shown in Figure 5b. For v=0.97c, the path would be as in Figure 5c.
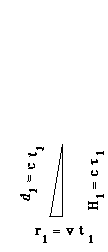
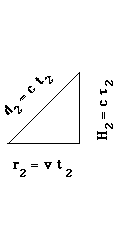
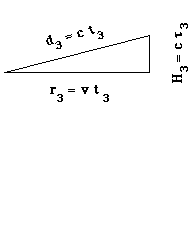
Figure 5a, v=0.2c Figure 5b, v=0.7c Figure 5c, v=0.97c
Suppose the rocket accelerates (increases its speed with time) smoothly from rest to v=0.2c to v=0.7c to v=0.97c. What will the light path look like? Draw it in on the following diagram, in which the path of the rocket and the light path in the rocket are given:
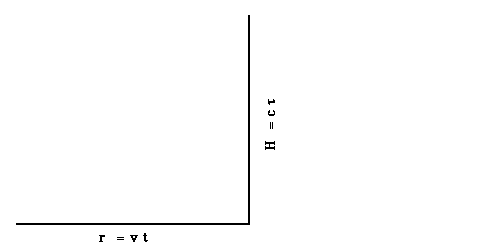
Figure 5d
If you sketched something roughly like the following, you are on the right track. If not, look back at Figure 5 a-c again and try to join them together smoothly.
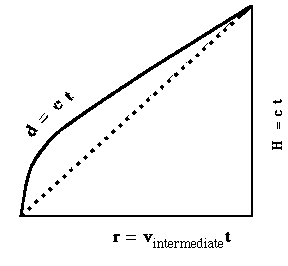
Figure 6
Had the space ship been moving at a constant velocity intermediate between zero and the final velocity, the path of the light would have been the hypotenuse of the triangle shown in Figure 6. Thus, the new problem reduces to the Special Relativistic case when then acceleration is zero.
One can see that Figure 6 is like Figure 2, but in the present case, with acceleration, the light path d = c t is not straight and is even longer than the hypotenuse, which you well know by now to be longer than H = c t. You can verify this by tacking string along the curve, mark the ends of the string and then pull straight to get a rough measure of the length. Since c is a constant this means that, again, t is greater than t. Thus, coordinate time is dilated relative to proper time when bodies are undergoing accelerated motion as well as when they are undergoing motion at constant velocity.
The Principle of Equivalence
Einstein founded his General Theory of Relativity on the idea that acceleration due to thrusters
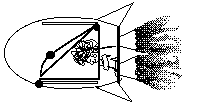
Figure 8a
and gravitational acceleration
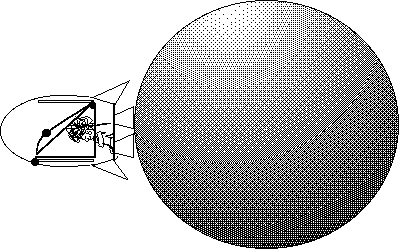
Figure 8b
must be indistinguishable since someone closed inside the space ship would not be able to tell the difference between the two.
This is called the Principle of Equivalence. Thus, the Earth-folks see a curved path for a light beam bouncing between mirrors on a space ship near a gravitationally attractive body just as they do for a space ship that is accelerating by firing its thrusters in empty space. So time gets stretched in precisely the same way for both space ships.
But is it Real?
Modern telescopes reveal a truly dramatic confirmation of the Principle of Equivalence. The light from distant galaxies will be gravitationally lensed by an intervening galaxy, galactic cluster, or black hole directly along the line of sight. This produces many arc-shaped images of the one galaxy in the photograph below.
Figure 6.
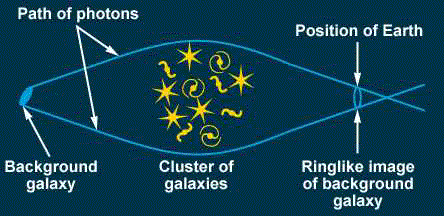
This is an exciting time to be alive because dramatic photographs of the affects of general relativity were not available three years ago.
Extracting the relationship between coordinate time and proper time due to acceleration near a massive body involves more complicated manipulation than we can do with cut-out paper. But the essential point is the same, space and coordinate time can be related to proper time. In this case the relationship is
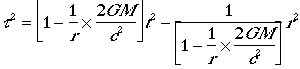(2)
As with time dilation, you may see a symbolic pattern emerging in the shape of the equations, even if you do not understand the details of the equations.
If we assume that the matter in the universe is homogenous and isotropic then we can immediately write down an equation describing the structure of the universe (space-time) itself. This equation can be pictured if we are willing to drop off one of the 3 spatial dimensions, just as we did in studying black holes. Robertson and Walker found there are three possible structures to space-time:
For the Robertson-Walker relation that describes the expansion of the universe, we might expect to see some quantity that changes with coordinate space and time multiplying the minus another quantity multiplying the term. It turns out that the correct relation is:
Flat and infinite k=0
jpeg – flat universe
jpeg – closed universe alias
Closed, finite but unbounded k=1
[The above figure is mine. See also
http://universe.colorado.edu/universe/tango/figures.qry?function=number&number=20.15]
jpeg–open universe
or open, curved, infinite, and unbounded, k=-1
(In mathematica: Plot3D[Sqrt[1+x^2] Sqrt[1-y^2] , {x, -1.5, 1.5}, {y, -.9,.9}])
[The above figure is mine. See also
http://universe.colorado.edu/universe/tango/figures.qry?function=number&number=20.14]
First consider a closed universe. Suppose we glue pennies on a balloon to represent galaxies and let the radius of the balloon, R, get bigger.
http://oposite.stsci.edu/pubinfo/pr/96/21/expand.jpg
We see that the galaxies are indeed moving apart from each other and, as Hubble saw, those furthest away move away at faster rates.
So the cosmic expansion of the universe is not due to a galaxy moving from "Los Angeles" to "New York", but is instead due to the fact that "Los Angeles" and "New York" are moving farther apart from each other as the surface of the balloon they are on gets inflated. The scale of the universe is expanding and drags the galaxies apart with it. Note that in such a scheme every galaxy would see every other galaxy receding, and we thus avoid the idea that we are at the center of the universe.
[Note that the size of the pennies does not change so our local rulers don’t grow with time.]
In that case the space is finite with a current proper-circumference L = 2pR, of 82 billion light years (one light year being the distance light travels in one year, which is nine trillion kilometers). Since this universe has no edge, if you waited 82 billion years, you would eventually see light from the back of your head that had traveled all the way around the hypersphere to your eyes.
R is actually a function of time, so when it is small, L is also small. This idea is the essence of the big bang. If now we see an explosion, and the size of the universe is what is exploding, at some point in time, the size of the universe must have been zero, a cosmic Black hole.
What caused it to explode? Our mathematics take us back in time to a tiny fraction of a second after the explosion. but the singular nature of the equations (division by zero) indicates that our theory is incomplete. It can’t say anything about the singularity or its prior state.
In the case of an open universe, the Cosmic Scale Factor still measures the expansion of the universe, the just isn’t a circumference to measure.
jpeg–open universe expansion
So what do you suppose causes the universe to be open or closed? What is causing a closed universe to pull itself into a sphere? Gravity – Mass.
The universe is open, flat or closed depending on how much mass there is in it. The critical density is about 1.1x10-29 g/cc (and scales as (Ho/75 km/s/Mpc)2.
pict– 1/Ho fg26_013 .pct
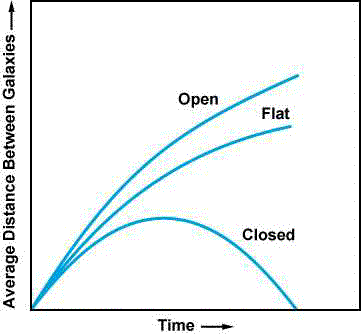
Size as a function of time for the three cases half hyperbola, parabola, ellipse
add tangent to where the three curves meet at present day: if space-time is empty, there is no deceleration.
All ages are less than or equal to to = 1/ Ho which we calculated as 13.4 Billion years for Ho=73 km/s/Mpc (9.8 Billion for Ho=100 km/s/Mpc) If closed, 7.5 billion , if only the mass of the galaxies is included, and the universe is open, it is .96 times 1/ Ho = 13 billion years.
Big Crunch
Edwin Hubble found a linear relation between how fast galaxies are moving away from us and how far away they are.
Taking his idea and using current distance measurements one would find that galaxies those at 1000 Mpc as moving away with a velocity of 73,000 km/s ± 6,000km/s
Draw it. Add on closed, critical, open tails curving up, in sequence to the right, respectively.
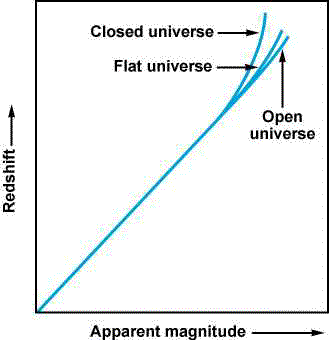
http://universe.colorado.edu/universe/tango/figures.qry?function=number&number=20.16
Helium formation
At high temperatures the processes for transforming neutrons into protons are equally likely as the reverse processes.
but at low temperatures and densities the one-body reaction is more probably, so the universe begins with equal numbers of protons and neutrons but between 1012 K at 10-3 s and 1.3 × 109 K at 98 s neutrons decay so that there are only 1/4 as many of them as protons. At this temperature helium synthesis can proceed without the helium being immediately ripped apart again, and over the next 2080 s virtually all of these neutrons are captured to create helium nuclei.
Thus we should see about 3/4 hydrogen and 1/4 helium in the universe, exactly what we do see.
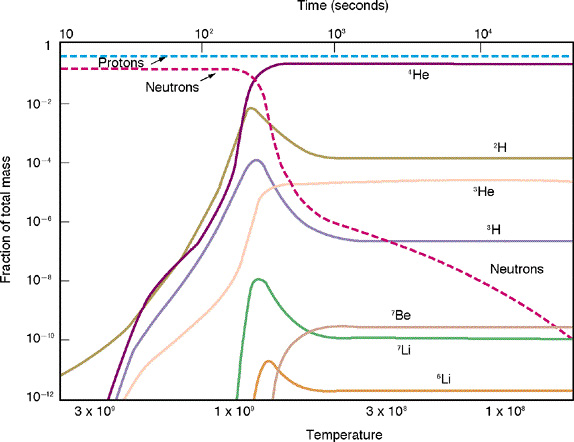
http://universe.colorado.edu/universe/tango/figures.qry?function=number&number=20.18
The earliest we will be able to see is back to when the temperature was 4500 K, (z=1500)
jpeg– CosmicTimeline_gr.jpg alias
http://www.nap.edu/readingroom/books/cosmology/1.html#CosmicPictureIllustration
See also
http://www.damtp.cam.ac.uk/user/gr/public/bb_history.html
As we look out 12 billion years in two opposite directions, we see microwave radiation that has exactly the same temperature, 2.735 degrees K. This is the remnant of the big bang fireball that has expanded and cooled over the 13 billion years of the universe’s existence.
gif–COBE anisotropy.gif
http://universe.colorado.edu/universe/tango/figures.qry?function=number&number=20.08
see also
http://universe.colorado.edu/universe/tango/figures.qry?function=number&number=20.07
http://oposite.stsci.edu/pubinfo/pr/1998/01/
Now these two regions, separated by 24 billion lyr are not in causal contact with each other since light is the fastest means of communication, i.e., a sharing of temperature. So how do we account for the fact that the temperature is the same to one part in 400? (.007K)
It is supremely ironic that the study of the small-scale structure of the universe, of protons and electrons, should give us the answer to this cosmic scale uniformity. There are theories that unify the forces that govern the structure of hadrons such as protons and neutrons and the electrical forces at very high temperatures, such as would have been present in the big bang. As the primordial fireball cooled to 1028 K at 10-35 s after the universe exploded into being, these forces decoupled in a phase transition similar to water turning to ice.
Alan Guth has shown that the universe could slip into a quantum state very much like the degeneracy pressure of a white dwarf or neutron star, and there would be an intense outward pressure that would change the size of the universe from 10-25 cm to 10+25 cm: From 100 billion times smaller than a proton nucleus to 10 million parsecs between t = 10-35 s and t = 10-32 s!
That sure exceeds the speed of light! This is the only known way to explain the uniformity of the cosmic the cosmic microwave radiation.