THE BIG BAD UGLY ANSWER
The first formula is for the acute triangles. The B range is from
the intersection of (C^2-B^2)^.5 and B-1 up to C-1 and sums all of
the integers above (C^2-B^2)^.5 and below B-1. We had to use
floow functions and ceiling functions which rounded the irrational numbers
either up or down depending upon the need.
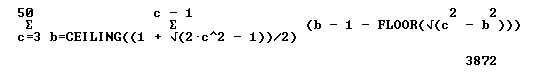
For obtuse it was a little harder because it had to be done in two pieces.
One sum is for B values above the intersection of (C^2-B^2)^.5 and B-1
and the other is for the integers below.
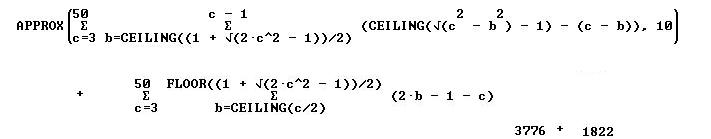
Acute Triangles: 3,872
Obtuse Triangles: 5598
Right Triangles: 20
Sum: 9490
Oh NO! You will notice that this number is quite close, but not quite
close enough to our total number of possible triangles.
This is because my formulas above are not quite right.
Suspected Reasons for This:
*Accidentally slipping right angles into the formula for
counting obtuses and acutes
*trouble at the intersection
point. I am not sure what is happening there
*Other formula errors.
Working with Ceilings and Floors is not a simple business.
I glad that I at least made it into the ballpark range.
BACK
BACK TO MAIN GAME
HOME