Sines
and Cosines...
...Revisited.
We just got done talking about Derivatives and
Anti-Derivatives, now let's go back and look how they apply to a function
that we discussed earlier.
Below, in Fig. 1.86, you can see the parent graph
y=a sin bx +c.
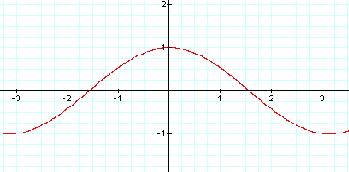
And, in Fig. 1.96, the parent graph y=a cos bx
+c, where a=b=1 & c=0.
Fig. 1.86
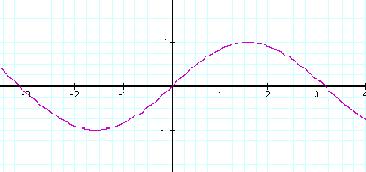
Fig. 1.96
Again, remember that the derivative of a function describes the slope
of that function at any given point. So let's take a look at how
that works for a Sine and Cosine function.

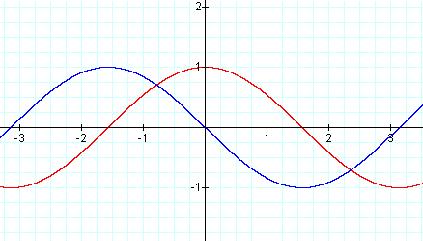
Above is shown the parent graph of f(x)=sinx
(purple) with it's derivative f'(x)=
cosx (Blue). You can see that
the rules for derivatives hold true. As f(x)'s
slope is increasing, so is f'(x). And
when f(x) is at a high point or low point,
where the slope is zero, f'(x) is intersecting
the x-axis at a zero.
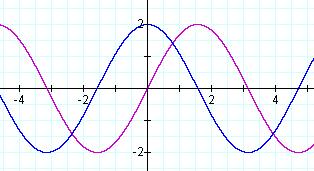
Just below is pictured g(x)= cos x, and
it's derivative g'(x)= - sin x.
And the same rules for derivatives hold true for the cosine funtion.
But let's take a look at what happens as we change the a, b, and c values
in each function and their respective derivatives.
Let's start with the sine function and see what happens as we change
a, b and c.
Below is f(x)= 2 sin x and f'(x)=
2 cos x.
You can see that just by changing the amplitude
of the parent graph it also changed the amplitude of the derivative.
I am pretty sure that's not hot news. I
should have predicted that one before looking at it.
I think the same will be true for cosine function.
Low and behold it's true. In the picture below g(x)=
.75 cos x, and g'(x)= -.75 sin x.
So far conjecture is true. The as you change the amplitude of
a sine/cosine function,
the amplitude of their derivative changes accordingly.
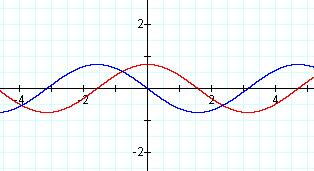
Now let's take a look at changing the b-value. If you remember
the b-value affects how many cycles in 2pi.
Below is f(x)= sin 2x. So there
will 2 cycles now where there used to be just one. Also pictured
is f'(x)= 2 cos 2x.
As you can see, when taking the derivative, we not only affected the
number of cycles, but also the amplitude.
What's interesting is how f'(x) is following
the rules of a derivative and describing the slope of f(x).
And how that is only made possible by increasing the amplitude. Neat...
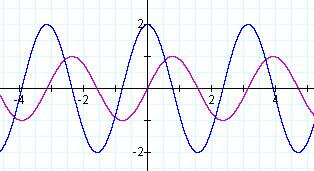
Below you can see that the same holds true for g(x)
and g'(x).
So we know that taking the derivative of a Sine/Cosine funcion with
b-value other than one, is goin to affect not only the # of cycles but
also the amplitude of the function.
Now the c-value...
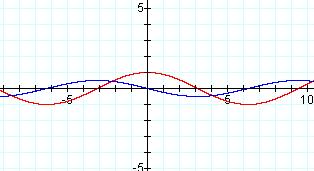
Below f(x)= sin (x + Pi) and f'(x)=
cos (x + Pi). So once again my conjecture held true.
The c-value held true in the derivative.
The same hold true for g(x)= cos (x + Pi/6)--
g'(x)= - sin (x + Pi/6). Which I guess
makes sense, since all we are doing is shifting the picture left and right.
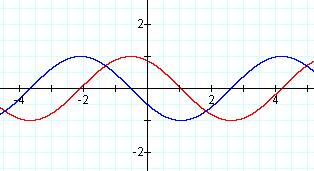
I wonder how that works for adding the two functions, f(x) + g(x), or
the composition of the two f(g(x)?.
Let's let h(x)= f(x)+g(x), where
f(x)= sin x and g(x)= cos x.
Like we found out before by adding the two funcions
we have basically just come up with a brand new parent equation, where
the rules for a, b, and c are the same.
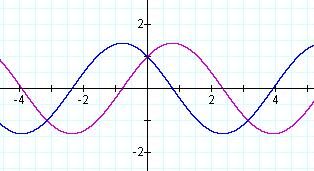
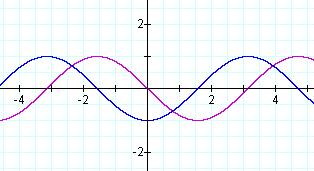
Below is the composition of the two functions, h(x)=f(g(x)).
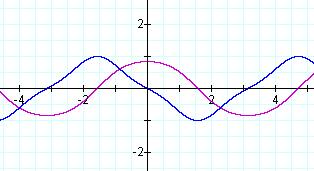
And look at what we found with the derivative. I am not even
sure how to describe that picture.
The derivative h'(x)= - sin x cos(cos x).
And once again the composition function has thrown me for a loop.
I wish I would have left myself some more time to further explore.
Possibly later...
Home / MTH
588 / Top O'
Page / Beginning
of Functions


