Some concepts and skills are presented in interchangeable forms. Cognitive flexibility is the ability to be literate in these multiple forms. For example, the same information can be presented in words (temperature in degrees C vs. temperature in degrees F), as an equation T C = (TF - 32)*5/9, as a table or as a graph. Experts "see" all of these forms as interchangeable, and switch between formats seamlessly.
Table 1. "Cognitive flexibility" exercise example. The instructor would prepare similar grids with different cells missing.
verbal algebraic chart table The temperature in Celsius goes from 0 at freezing to 100 at boiling. The temperature in Fahrenheit goes from 32 at freezing to 212 at boiling.
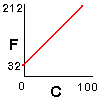C F 0 32 25 68 39 98.6 100 212
This type of cognitive flexibility can be taught using scaffolding. Students can be lead through examples in which the same information is presented in multiple formats with an explanation of each form. Then they can be given examples that are missing different forms of the information and then the instructor can provide only one form of the information and have students develop the other formats. A common test for understanding these skills are mixed format "story" problems in which the student has to identify what information that they need and then recognize that that information is available in one of the formats.
Table 2 lists some representational translations that might be required. Some of the simple changes are at the level of associations, remembering scientific terms that more precisely describe a common process. Although this may seem trivial, the translation in and out of newspaper and magazine language can be one of the crucial processes in the interpretation of environmental science into environmental policy and politics. Similalry, some translations into abbreviations or acronyms may seem trivial but the sheer number of these in a course may be overwhelming for some students.
Table 2. Representational changes involved in abstraction and application
Sometimes tools or processes are needed to make these different representations. This is important for student learning in two ways. First, it may not be a valid assumption that all students know how to do the simple transformation, i.e. they may not remember how to write an algebraic equation or they may not sense that a particular English sentence can be turned into an equation. These are different student learning problems that the student's inability to recognize that a particular English sentence and an algebraic equation are equivalent. It is important to build assessments for the simple skills into the use of the cognitive flexibility matrix.
The second reason that these tools are important to representation is that you might think you are asking students to remember (simple recall) of a particular piece of information when in fact some of them are using the tools to reconstruct the information. In many situtations, the latter response is desirable. You might rather have students rely on central principles and reconstruction of specifics as needed. This allows the student to incorporate new information and improved understanding with each new reconstruction. Some texts intentionally revisit the same problem to illustrate how the student's improved understanding leads to a better understanding (See Berry 1996 for example).
