poisson_photoinhibition.html
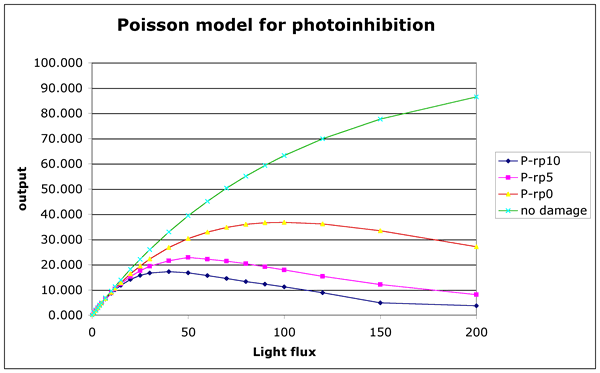
If a photon hits a site that is already closed it could do damage. The following simple simulation looks at 100 sites that have a mean probability that they will be hit based on the light flux. Three repair conditions are considered
no repair time - a second (or third) photon knocks out that site but it can recover and work in the next time
5 turnover time units to repair - it takes 5 times the time for one normal turnover to repair the site
10 turnover time units to repair
no damage - a poisson model that allows multiple hits on the site, but only one would be active.
The difference between "no repair time" and "no damage" is that in the "no repair time", multiple hits knock out the site. You can see how the curve slopes off, even with out repair, this is indicative of the number of sites that are being hit by multiple photons during one turnover time.
Figure

Data table
| Experimental output | multiple hit | |||
| E | P-rp10 | P-rp5 | P-rp0 | no damage |
| 0 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.990 | 0.990 | 0.990 | 0.995 |
| 2 | 1.956 | 1.959 | 1.960 | 1.980 |
| 3 | 2.900 | 2.906 | 2.911 | 2.955 |
| 4 | 3.816 | 3.831 | 3.843 | 3.921 |
| 5 | 4.705 | 4.733 | 4.756 | 4.877 |
| 7 | 6.392 | 6.466 | 6.527 | 6.761 |
| 10 | 8.683 | 8.822 | 9.048 | 9.516 |
| 12 | 10.042 | 10.367 | 10.643 | 11.308 |
| 15 | 11.827 | 12.405 | 12.911 | 13.929 |
| 20 | 14.144 | 15.300 | 16.375 | 18.127 |
| 25 | 15.721 | 17.604 | 19.470 | 22.120 |
| 30 | 16.680 | 19.360 | 22.225 | 25.918 |
| 40 | 17.254 | 21.510 | 26.813 | 32.968 |
| 50 | 16.736 | 22.850 | 30.327 | 39.347 |
| 60 | 15.700 | 22.135 | 32.929 | 45.119 |
| 70 | 14.495 | 21.414 | 34.761 | 50.341 |
| 80 | 13.320 | 20.368 | 35.946 | 55.067 |
| 90 | 12.250 | 19.157 | 36.591 | 59.343 |
| 100 | 11.210 | 17.884 | 36.788 | 63.212 |
| 120 | 8.860 | 15.383 | 36.143 | 69.881 |
| 150 | 4.867 | 12.120 | 33.470 | 77.687 |
| 200 | 3.722 | 8.074 | 27.067 | 86.466 |