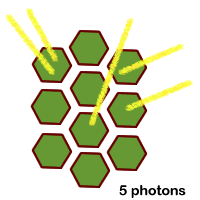
Imagine that you have 10 pigments (targets) that photons can hit.

Each target takes a certain length of time to get ready to absorb the next photon. Let's just set that time period to "1 unit of time".
During that short time period, a number of photons hit the area. Even though they are random, they aren't necessarily evenly distributed over the area during that short time. Each event (photon hitting a target) is an independent event. You could get all of photons hitting one of the ten targets.
In this example, 5 photons the area but two hit the same target. The cell would be able to only use 4 of the 5.
You can imagine a simulation of this if you had six targets and you rolled a dice to find out which target each photon was going to hit. You wouldn't necessarily get a 1,2,3,4,5 and a 6 for six rolls (i.e. 6 photons).
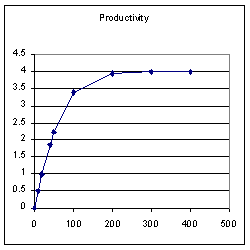
In order to get the maximum output out of this set of photosynthetic targets, how many photons would have to hit the area? You could try this with dice, or we could simulate it with an Excel spread sheet.
Download the simulation of Poisson distribution.
Fitting the curve.
For reasons that we aren't going into here (because I don't know them); we can fit the curve of the Poisson distribution of n events on T targets by the equation TANH(n/T).
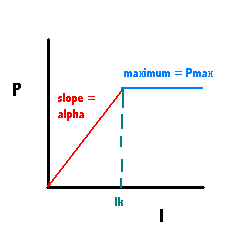
In photosynthesis we will use this form of the equation where the number of targets (T) is indicated by the linear extrapolation of alpha to Pmax - called Ik and the light intensity is I. You will see the term I/Ik or I/(alpha/Pmax)