Pablo Baldivieso
                                              Assignment 7

Problem 1

Conic Construction using Geogebra   The link is here







Problem 2

Mini-tutorial  Geogebra

1. Download Geogebra from http://www.geogebra.org/cms/en/download.
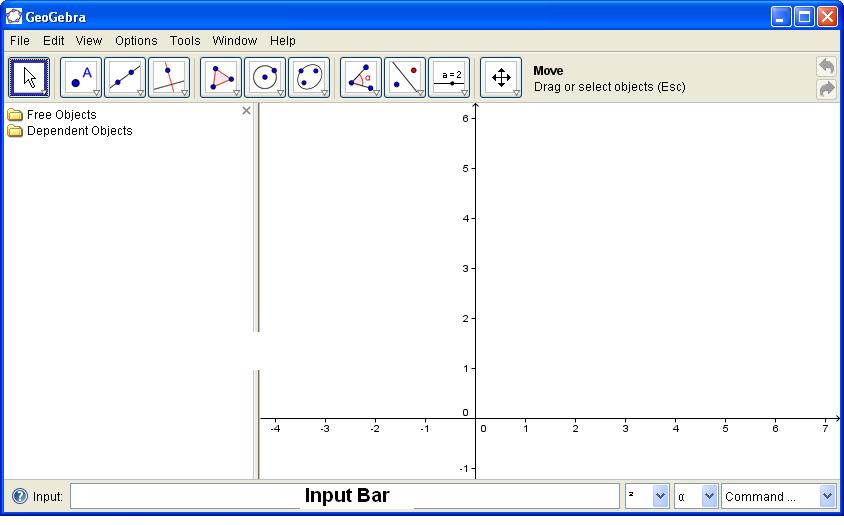
2. The Geogebra's screen, and the input bar looks like the following picture:
 

3. We are interested in constructing an ellipse and a hyperbola using the general forms  x^2/a^2 + y^2/b^2 = 1, x^2/a^2 - y^2/b^2 = 1.
4. The parameters a and b are adjustable. Type in the Input Bar: a =1, press enter, b = 1 press enter.
5. Geogebra recognizes functions and some common conic equations, so you can type either x^2/a^2 + y^2/b^2 = 1, x^2/a^2 - y^2/b^2 = 1 in the Input Bar.




Problem 3

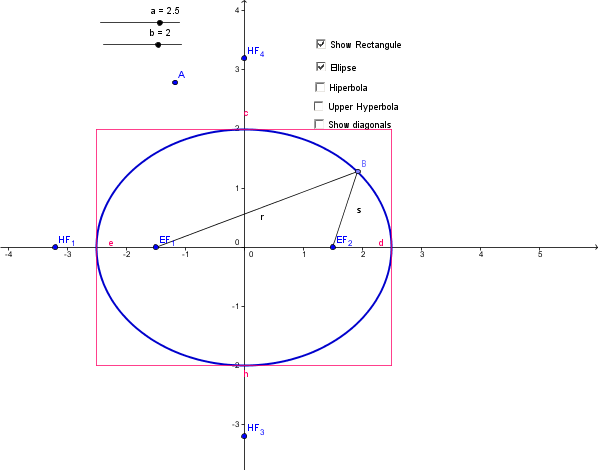
1. Fireplace Arch. A fireplace arch is to be constructed in the shape of a semi-ellipse. The opening is to have a height of 2 feet at the center and a width of 5 feet along the base (see figure). The contractor draws the outline of the ellipse by the string method. Where should the tacks be placed and what should be the length of the piece of string?
The tacks should be placed on the ellipse Foci which in the constructions are points EF1 and EF2. It easy to observed that the the distance between these two poins is equal to 3 feet.
To determine the length of the string using the construction we need to create a point on the ellipse and two line segments, then we can use the tool command Distance to measure the length of the two segments.




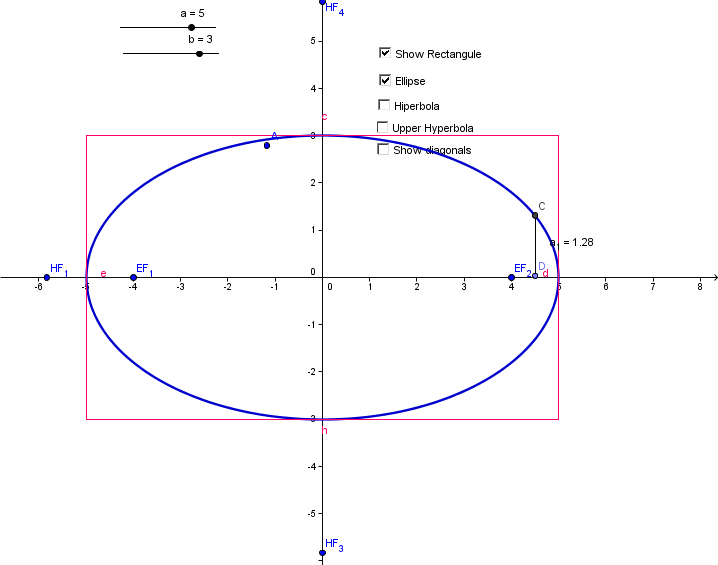
2. Mountain Tunnel. A semi-elliptical arch over a tunnel for a road through a mountain has a major axis of 100 feet, and its height at the center is 30 feet (see figure). Determine the height of the arch 5 feet from the edge of the tunnel. How did you use your construction to determine the answer?
For this problem since the dimensions of the tunnel are much larger than our first construction we can either rescale the dimension or change the parameters fit the actual dimensions of the tunnel. So I will rescale the construction so the 100 feet become 10 units in the construction.
So if we want to find the hight at 45 feet from the center we can draw a vertical line at x = 4.5. then we can measure the hight from the x-axis to the intersection of x=4.5 and the ellipse. I obtain a distance equal to 12.8 feet.



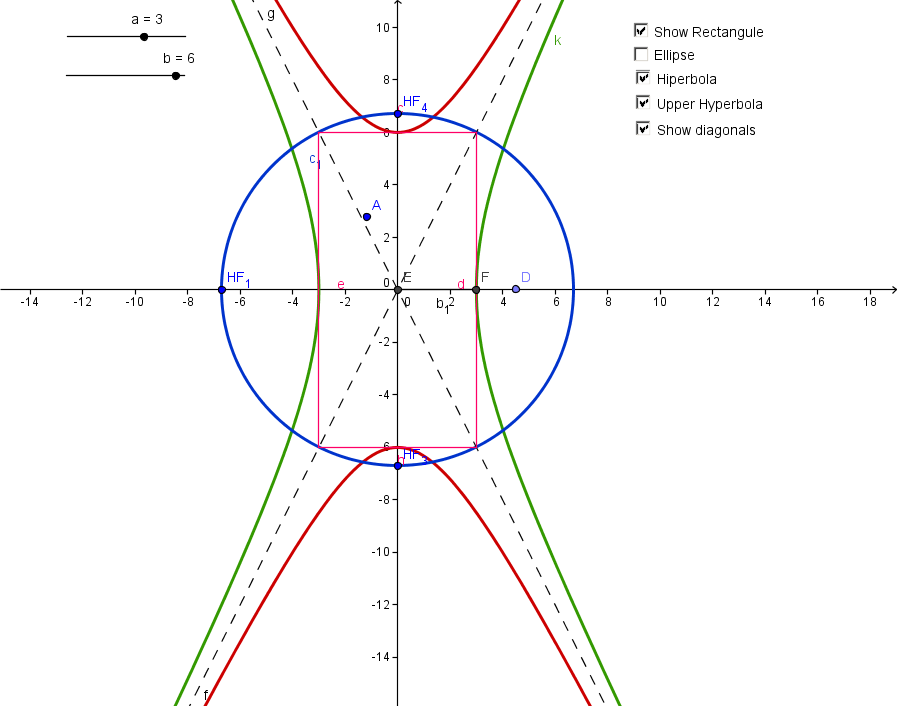
3. Explain how you would use your construction to graph the conic 4x^2 - y^2 = 36 ?  Using your construction find the vertices and foci of the conic to two decimal places.

If we divide each term by 36 we have x^2/9-y^2/36 = 1 or x^2 / 3^2 - y^2 / 6^2 = 2. so a = 3 and b = 6.
We have an hyperbola and we can plot it using our construction setting a = 3 and b = 6. The vertices are located at (3,0) and (-3,0) and the foci are located at + / - sqrt(a^2+b^2) = +/- 6.71 or in coordinates (-6.71, 0) and (6.71, 0).






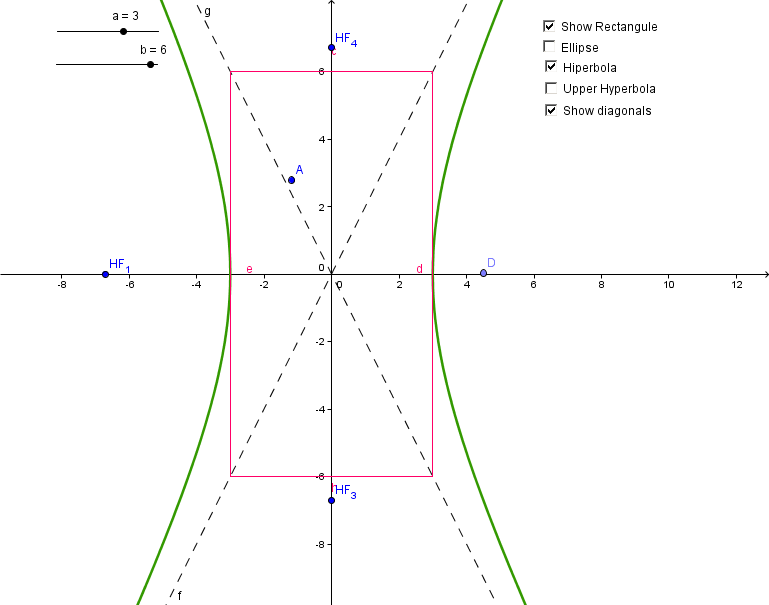
4. Construct a circle centered at the origin (or (h,k) if translated) through the hyperbola focus on the positive y axis. What other points does the circle pass through?
If the circle is centered at the origin and passes through the focus of the hyperbola, the circle passes through the vertices of the rectangle.