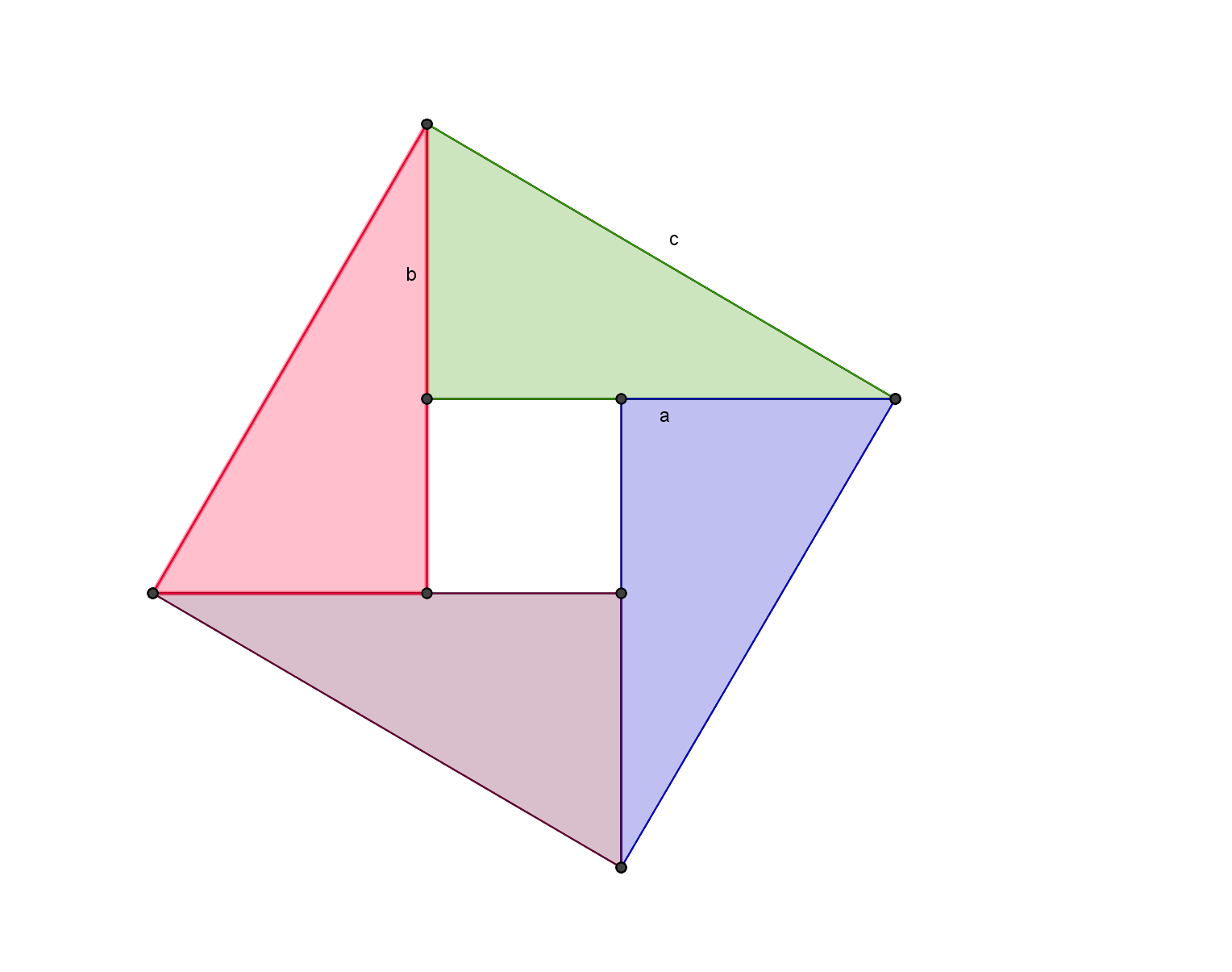Assignment 4                                                         Pablo Baldivieso

Problem One

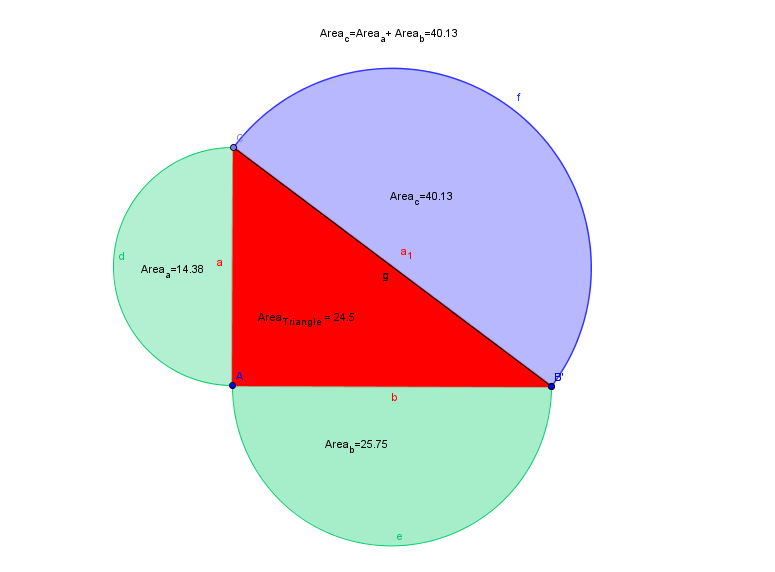
The generalized pythagorean  theorem holds for semicircles.



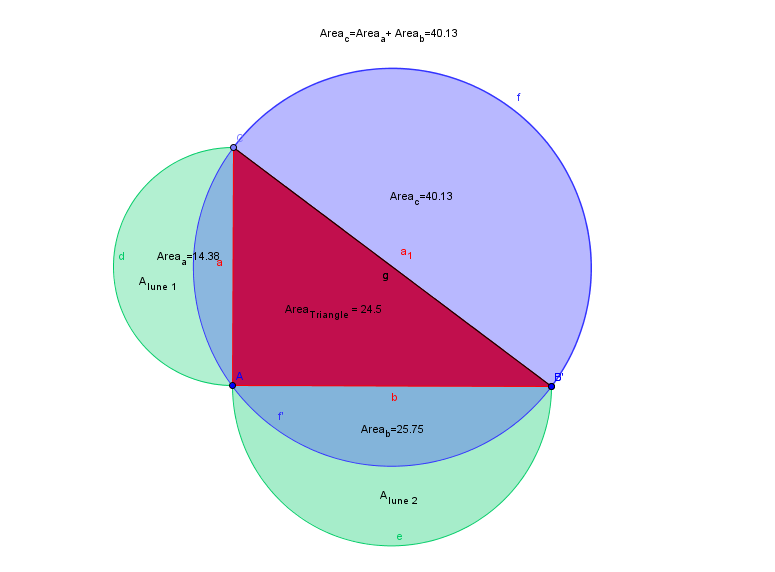
If we mirror the semicircle over the hypotenuse we create two lunes. The Area of the triangle is equal to the sum of the areas of the two lunes.

Define the following:
Area_c = Area of the hypotenuse semicircle
Area_a = Area of leg_a semicircle
Area_b = Area of leg_a semicircle
a* = area between the leg_a and the mirrored semicircle.
b* = area between the leg_b and the mirrored semicircle.
So:
A_lune1 = Area_a - a*
A_lune2 = Area_b - b*

Area_c = Area_a + Area_b     (Generalized Pythagorean Theorem)

We observed from the picture that the following relation holds:
Area_c = Area_triangle + a* + b*
so
Area_a + Area_b = Area_triangle + a* + b*
-->    (Area_a-a*) + (Area_b-b*) = Area_triangle
 -->    (A_lune1) + (A_lune2) = Area_triangle.
The GeoGebra file is here.




Problem Two

The Geogebra file is is here

The Pythagorean Theorem c^2 = a^2 + b^2.
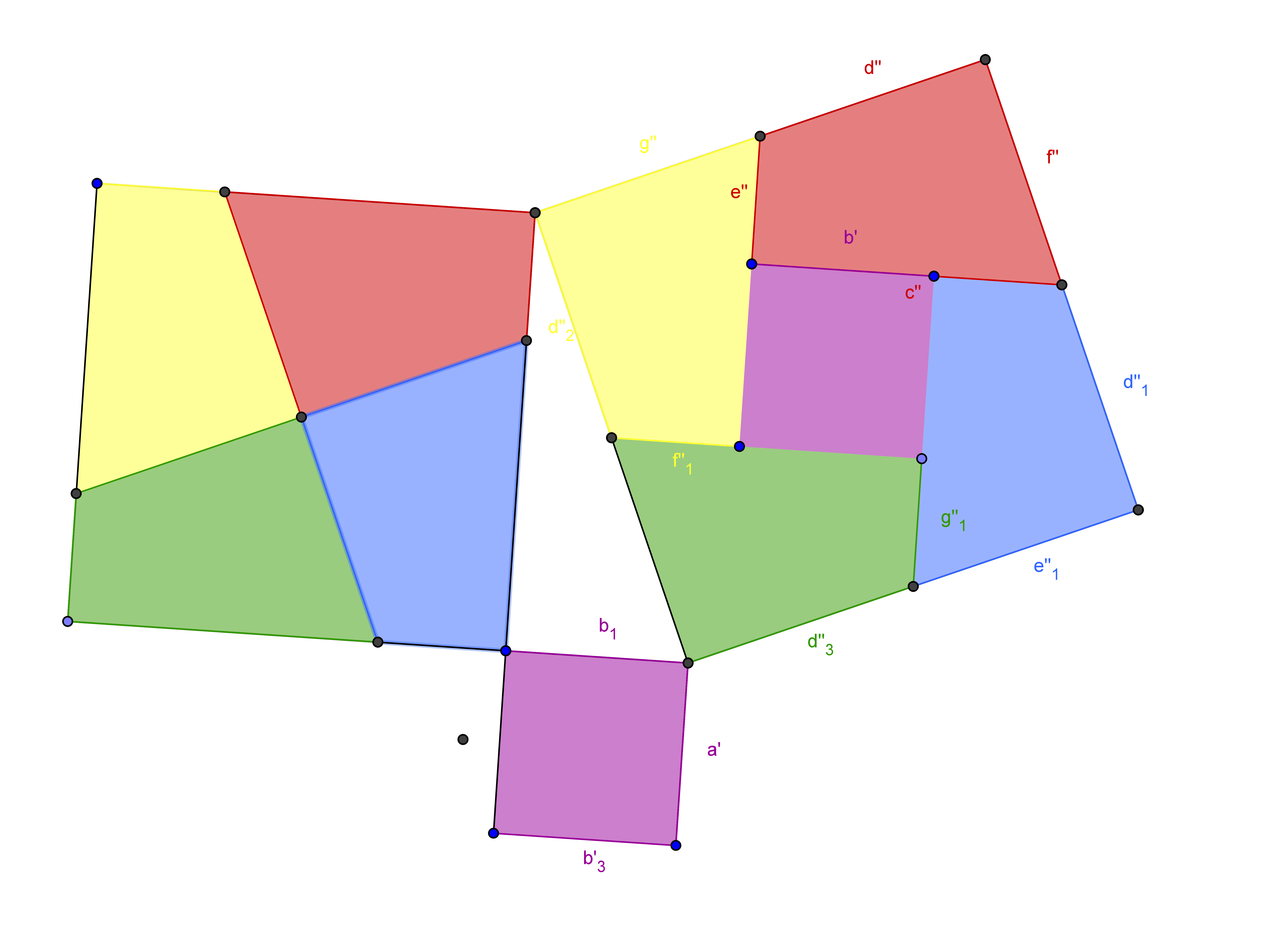
Create a resizeable right triangle.
Create an outside square on each leg and the hypotenuse of the triangle.
Find the center of the square from the larger leg of the triangle. Then draw two lines through the center of the square, one that is parallel and one that is perpendicular to the hypotenuse. Color the 4 polygons created by this method.
Translate the colored polygons inside the large square off the hypotenuse so that all five pieces fit perfectly inside with no overlapping.


Problem Three

Here is another construction proof of the pythagorean theorem:

Construct four right triangles:






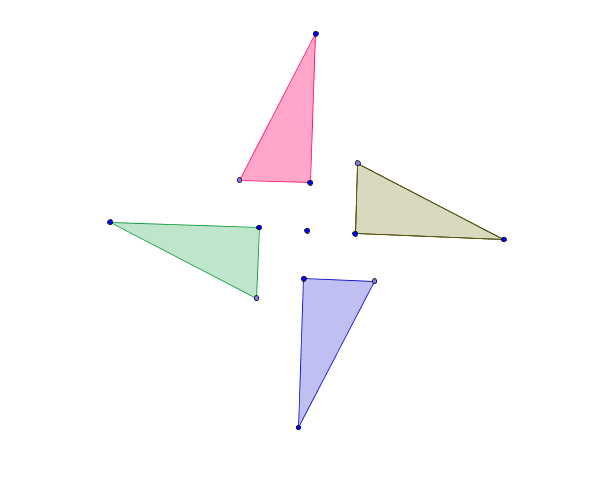
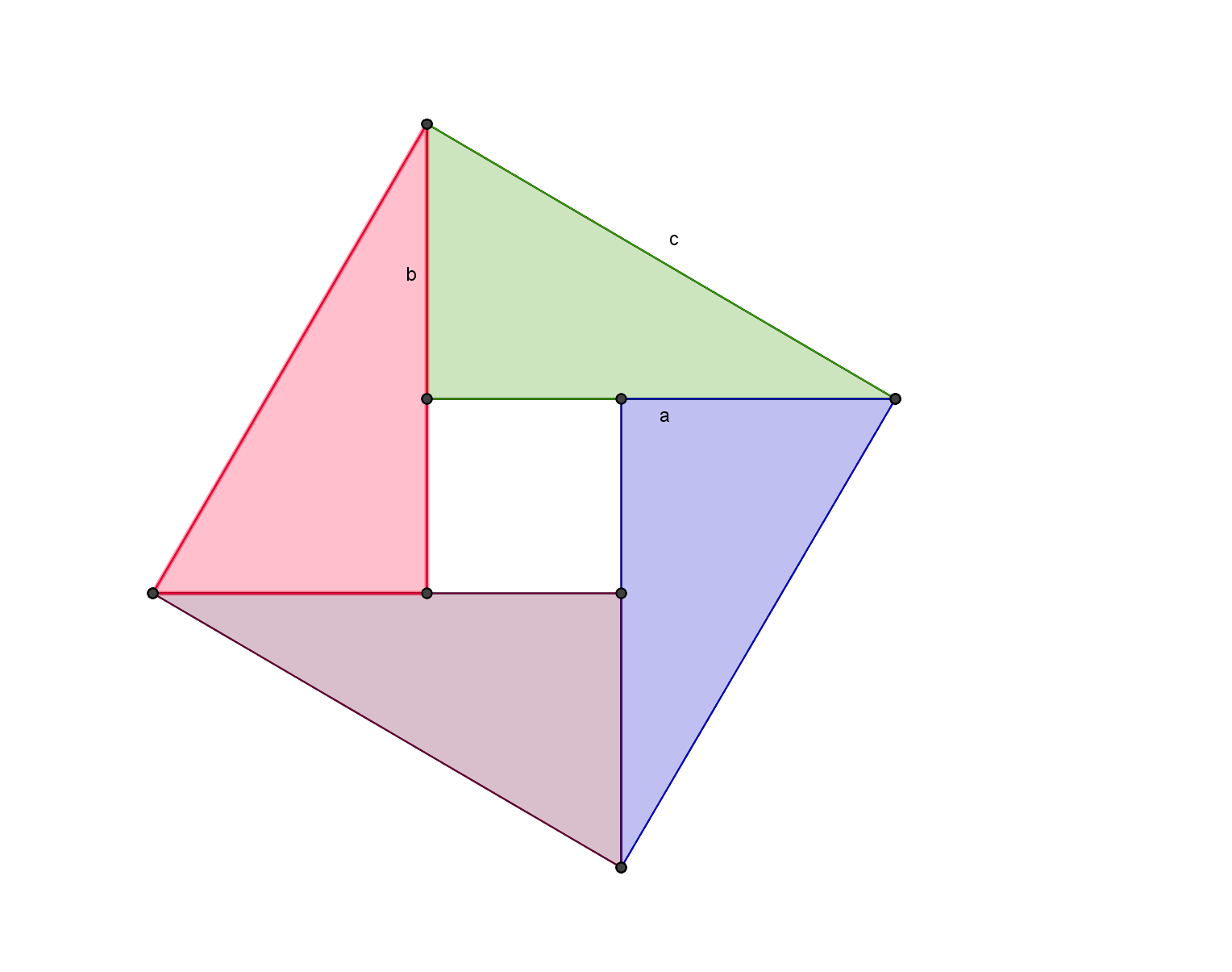
The area of the square, c^2, is equal to the area of the four triangles plus the square in the center. Note that (a-b)^2 is the area of the little square in the center. The area of the triangles is (1/2)ab*4 which is 2ab.
So c^2 = 2ab + (a-b)^2
            =  2ab +a^2 - 2ab + b^2
            = c^2 +b^2
The GeoGebra file is here