Coding of Categorical Predictors and ANCOVA
Equivalence of Regression and ANOVA
Testing whether there is a
mean difference between two groups is equivalent to testing whether there is an
association between a dichotomous independent variable and a dependent
variable. Thus, regression analysis can
test hypotheses which are tested with ANOVA.
The simplest example is the comparison of two groups (represented by an
independent variable with two values or “levels”) using ANOVA (or a
t-test). If the independent variable, X,
significantly predicts the dependent variable, Y, we would also find a
significant mean difference on Y between the two groups of independent
variable, X. The difference
between the two approaches is mainly that the regression approach does not
appear to provide information about the means in the two groups. This is not
entirely true, because we can obtain information about the mean from the
intercept (a.k.a, the “constant”).
The Intercept and Means
Remember
that to compute the intercept, we can use the following formula:
![]()
This
tells us that the intercept, a, is a function of the mean of the
dependent variable, ![]() , the regression coefficient, b, and the mean of the
independent variable,
, the regression coefficient, b, and the mean of the
independent variable, ![]() . If we were to use
the deviation form of X (usually denoted by x) where the X scores are recomputed by
subtracting the mean (
. If we were to use
the deviation form of X (usually denoted by x) where the X scores are recomputed by
subtracting the mean (![]() ), the meaning of the intercept changes. Because the mean of the deviation score, x, is now 0, the intercept will be equal the mean of
the dependent variable,
), the meaning of the intercept changes. Because the mean of the deviation score, x, is now 0, the intercept will be equal the mean of
the dependent variable, ![]() :
:
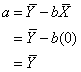
So,
depending on how we compute X, the intercept has different meanings.
Dichotomous X
Now,
back to the idea that regression and ANOVA are equivalent. In the case in which
X is a dichotomous variable (two values), such as gender, it has two
possible values. Because the values,
male and female, are qualitatively different, we can code the gender variable
any number of ways (e.g., 1=female, 2=male; or 0=female, 1=male etc.). If we choose a coding scheme for X
such that the mean will be zero, then the intercept will be the mean of the
full sample (males and females combined), sometimes called the “grand mean”.
Effect Coding
One
way of making the mean 0 when X is dichotomous is to code the two groups as –1
and +1. This is called effect
coding. If effect coding is used,
the intercept will be equal to the grand mean of Y, ![]() . Note that this
assumes that there are equal numbers of
–1s and +1s (I’ll return to this point in a minute). If we use effect coding, the results will be
identical to ANOVA results. That is,
F-test for the simple regression equation (test of R2) will
be equal to the square root of the F-test obtained from the ANOVA. Note that the t-test of b will also equal
. Note that this
assumes that there are equal numbers of
–1s and +1s (I’ll return to this point in a minute). If we use effect coding, the results will be
identical to ANOVA results. That is,
F-test for the simple regression equation (test of R2) will
be equal to the square root of the F-test obtained from the ANOVA. Note that the t-test of b will also equal![]() , and the R2 from the regression will equal
h2
from the ANOVA.
, and the R2 from the regression will equal
h2
from the ANOVA.
In
ANOVA, we examine group differences by examining how the group means vary
around the grand mean. You can see this
when we calculate the sum of squares for the main effect for the independent
variable, SSA.
![]()
Where
![]() is the mean of each
group and
is the mean of each
group and ![]() is the grand
mean. In regression, the effect coding
reproduces the idea of the difference between each mean and the grand mean by
the use of –1 and +1 values for the two independent variable groups. The regression slope, b, represents
the deviation of each group mean from the grand mean. Thus the F for the R2 from the
regression test is the same as the F for the ANOVA test.
is the grand
mean. In regression, the effect coding
reproduces the idea of the difference between each mean and the grand mean by
the use of –1 and +1 values for the two independent variable groups. The regression slope, b, represents
the deviation of each group mean from the grand mean. Thus the F for the R2 from the
regression test is the same as the F for the ANOVA test.
![]()
Dummy Coding
When 0 and 1 are
used instead of –1 and +1, it is referred to as dummy coding. If X is coded as 0 and 1, the
intercept will be equal to the mean of the group coded 0. For example, if males are 0 and females are
1, the intercept will represent the mean for males. The reason that the
intercept is the mean of the zero group is because, in the regression equation,
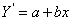 , the intercept, a, is the value of Y when X
equals zero. If males are coded 0, then
the intercept will represent the average score for males. This coding does not change the general
equivalence of ANOVA and regression, because the F tests will be
identical. The slope coefficient will be
different in the effect and dummy coding examples (although the standardized slope
and the significance won’t be different).
More specifically, because there is a two-point difference between –1
and +1, the slope will be half as large as when 0 and 1 are used. This becomes more complicated with more than
two groups, but the ANOVA equivalence is always maintained with an effect
coding scheme. To get the mean for each
of the groups, one could do two regression runs switching the dummy codes of 0
and 1.
, the intercept, a, is the value of Y when X
equals zero. If males are coded 0, then
the intercept will represent the average score for males. This coding does not change the general
equivalence of ANOVA and regression, because the F tests will be
identical. The slope coefficient will be
different in the effect and dummy coding examples (although the standardized slope
and the significance won’t be different).
More specifically, because there is a two-point difference between –1
and +1, the slope will be half as large as when 0 and 1 are used. This becomes more complicated with more than
two groups, but the ANOVA equivalence is always maintained with an effect
coding scheme. To get the mean for each
of the groups, one could do two regression runs switching the dummy codes of 0
and 1.
Analysis of Covariance (ANCOVA)
ANCOVA is a simple extension
of ANOVA. ANCOVA simply means covariate
is included in the analysis. In other
words, instead of just using our dichotomous independent variable, X, as the predictor, we also use another
predictor, X2. X2
can be a continuous predictor. Thus,
the difference between the two groups (e.g., males and females) can “adjust” or
control for the other independent variable.
In our multiple regression equation, the intercept value adjusts for or
partials out the effect of the covariate, X2.
More than Two Groups
When more than two groups
are involved, using regression to approximate an ANCOVA analysis becomes a
little more complicated. Generally, it
is simple to test the same overall hypotheses that there are differences among
several groups using regression analysis, but getting the output to be exactly
identical to that obtained from an ANCOVA analysis using GLM is a little bit
tricky. One needs to develop an effect
coding of the categorical independent variable that will produce.
With more than two groups
one needs g-1 indicator variables (or more generally called dummy variables),
where g is the number of groups. If
there are three groups, two indicator variables are needed. If there are four groups, three indicator
variables are needed. One can still
choose dummy or effects coding schemes to give different meanings to the
intercept and slope coefficient. Here
are two examples, one dummy and one effect coding for three groups with six
cases.
|
Original coding of X |
Dummy variable 1 |
Dummy variable 2 |
Effect variable 1 |
Effect variable 2 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
2 |
1 |
0 |
-1 |
1 |
|
2 |
1 |
0 |
-1 |
1 |
|
3 |
0 |
1 |
0 |
-2 |
|
3 |
0 |
1 |
0 |
-2 |
When to use ANOVA or ANCOVA vs. Regression
Because ANOVA and regression
are statistically equivalent, it makes no difference which you use. In fact, statistical packages and some text
books now refer to both regression and ANOVA as the General Linear Model,
or GLM. You will find the same answer
(provided you have tested the same hypothesis with the two methods). Regression analysis is a more flexible
approach because it encompasses more
data analytic situations (e.g., continuous independent variables).