Hypersphere
From Wikipedia, the free encyclopedia
In mathematics, a
hypersphere is a sphere which has dimension 3 or
higher. The term n-sphere is often used for a sphere of any
dimension. An origin-centered sphere of radius R consists of all
points in n-dimensional Euclidean space for
which the sum of the squares of every coordinate is constant. The
constant is R2, and its square root
is the Euclidean distance of every point on the sphere from the origin. The set
of all points on this sphere has dimension n-1, so it is called the (n-1)-sphere
and is denoted 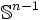 . It
may be written as
. It
may be written as ![[x_1,x_2,\ldots,x_n]](Hypersphere - Wikipedia_files/e27f46ff43ef0fb1072b8630b3149741.png) where
where
The above hypersphere in n-dimensional Euclidean space is an example
of an (n−1)-manifold. For example, an
ordinary sphere in three dimensions is a 2-sphere, denoted by 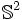 ; the
1-sphere being a circle, and the 0-sphere is the
end points of an interval. Of course,
translating the coordinates (i.e. moving the center around) doesn't change the
analytic or geometric properties of the sphere.
; the
1-sphere being a circle, and the 0-sphere is the
end points of an interval. Of course,
translating the coordinates (i.e. moving the center around) doesn't change the
analytic or geometric properties of the sphere.
Contents |
Hyperspherical volume
The hyperdimensional volume of the space which a (n-1)-sphere encloses (the n-ball) is:
where Γ is the gamma function. (For even n, Γ(n / 2 + 1) = (n / 2)!.)
The "surface area" of this sphere is
The interior of a hypersphere, that is the set of all points whose distance from the centre is less than R, is called a hyperball, or if the hypersphere itself is included, a closed hyperball.
Hyperspherical volume - some examples
For small values of n, the volumes, Vn , of the unit n-ball (R = 1) are:
-
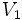
= 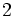
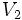
= 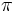
= 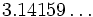
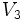
= 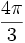
= 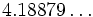
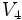
= 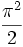
= 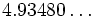
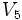
= 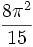
= 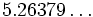
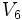
= 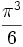
= 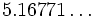
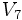
= 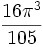
= 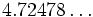
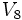
= 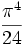
= 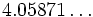
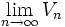
= 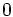
If the dimension, n, is not limited to integral values, the hypersphere volume is a continuous function of n with a global maximum for the unit sphere in "dimension" n = 5.2569464... where the "volume" is 5.277768...
Hyperspherical coordinates
We may define a coordinate system in an n-dimensional Euclidean space which is analogous to the spherical coordinate system defined for 3-dimensional Euclidean space, in which the coordinates consist of a radial coordinate r, and n-1 angular coordinates {φ1,φ2...φn-1}. If xi are the Cartesian coordinates, then we may define
The hyperspherical volume element will be found from the Jacobian of the transformation:
and the above equation for the volume of the hypersphere can be recovered by integrating:
Stereographic projection
Just as a two dimensional sphere embedded in three dimensions can be mapped onto a two-dimensional plane by a stereographic projection, an n-dimensional hypersphere can be mapped onto an n-dimensional hyperplane by the n-dimensional version of the stereographic projection. For example, the point [x,y,z] on a two-dimensional sphere of radius 1 maps to the point [x / (1 − z),y / (1 − z)] on the xy plane. In other words:
Likewise, the stereographic projection of a hypersphere 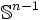 of
radius 1 will map to the n-1 dimensional hyperplane
of
radius 1 will map to the n-1 dimensional hyperplane 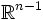 perpendicular to the xn axis
as:
perpendicular to the xn axis
as:
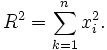
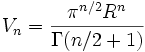
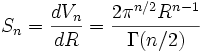
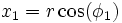
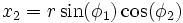
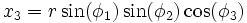

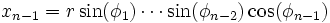
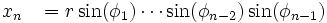
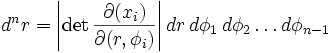
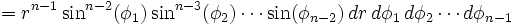
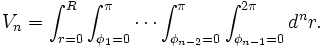
![[x,y,z] \mapsto \left[\frac{x}{1-z},\frac{y}{1-z}\right]](Hypersphere - Wikipedia_files/5c1d8f867f1f198f5c3c203f295ec978.png)
![[x_1,x_2,\ldots,x_n] \mapsto \left[\frac{x_1}{1-x_n},\frac{x_2}{1-x_n},\ldots,\frac{x_{n-1}}{1-x_n}\right]](Hypersphere - Wikipedia_files/a84d0bc1b3aa403d237a1dcef32927d9.png)

