The following general discussion and the R material are based on the content presented in my book on Pages 22-24 and 43-46:
R Data Analysis without Programming: Explanation and Interpretation, 2nd edition, Routledge, January, 2023.
Introduction
We begin with the fundamental concept: The analysis of data.
Data analysis
The analysis of the data values of one or more variables.
All data analysis computations are done today using the computer, yet people analyzed data well before computers were invented. A variable’s conceptual meaning and data values exist apart from the computer. This distinction applies to all data analysis software.
Examine read data before analysis
Whether using R, Python, Excel, Tableau, or any other system, we need to understand how our data values are digitally stored and how that representation matches our conceptual definitions.
At the most general conceptual level, we have variables that represent continuity and variables that define discrete non-numerical categories. A more complete expression of this distinction follows.
Two Classes of Variables
Continuous or categorical variables are analyzed differently, so it is essential to differentiate between them before beginning an analysis. To complicate that differentiation, numerical values can represent both types of variables. Moreover, even for continuous variables, the numeric data values can represent different levels of quality, permitting different types of numerical operations.
Always identify your continous and categorical variables
Before analysis begins, after reading data into the analysis system, distinguish between the continuous and categorical variables and their corresponding properties.
These issues should be understood before analysis begins. The most general lesson is that numeric data values can represent different levels of numeric quality. In extreme cases, a numeric data value may not even represent a number.
Continuous Variables
The values for a continuous variable, sometimes called a quantitative variable, are ordered along a quantitative continuum, which is the abstraction of the infinitely dense real number line.
Continuous variable
Values of the variable are ordered along an infinitely dense numerical continuum.
Choose any two values and find unlimited numeric values between them. Examples of continuous variables for a person are Age, Salary, and extent of Agreement with an opinion about some political issue; for a car, MPG and Weight; and for a light bulb, Mean Number of Hours until Failure and Electrical Consumption per Hour (kilowatt hours). A continuous variable is sometimes called a quantitative variable.
Continuous data values only approximate actual values
Distinguish between a continuous variable’s actual values and the data values that emerge from measuring those values.
Measurement categorizes data values into specific groups. The value of the variable as it exists always differs from the value of its measurement, the data value. Nothing, for example, weighs exactly 2 pounds, 2.01 pounds, or even 2.0000000001 pounds. The actual weight may theoretically be stated as an indefinitely large number of decimal digits. In contrast, indicate a measurement to a specific level of precision, such as, for weight, to the nearest pound, ounce, or gram. Measurement groups all similar weights together, approximating the true weight to the nearest pound or whatever the unit of measurement.
Interpret the data values measured on a numeric scale for a continuous variable according to one of two types: Ratio data and interval data. Ratio data follow a numeric scale with the usual properties assigned to numbers.
Ratio data
Data organized according to a numeric scale with a fixed zero point and proportionality.
Two different ratio data values can be compared by their ratios: 20 is twice as much as 10. Equal intervals of measurement separate values that are equal distance from each other. For example, the distance between 21 and 22 represents the same underlying difference for 22 and 23.
Just because you have numerical data for a variable does not imply that the data values exhibit the standard properties of numbers on a number line, that is, ratio data. A weaker numerical scale applies to interval data.
Interval data
Data organized according to a numerical scale without a fixed zero point but equal intervals.
Interval data maintains the equal interval property of ratio data but does not have a fixed, natural zero point. The classic example of two alternative interval scales compares Fahrenheit and Celsius temperatures. As an example, compare Fahrenheit and Celsius temperatures. Each temperature scale, for example, has a different value of zero regarding the magnitude of the temperature. 0\(^{\circ}\)F is not the same temperature as 0\(^{\circ}\)C.
Because 0\(^{\circ}\) is arbitrary, ratio comparisons for interval data are not valid; 20\(^{\circ}\)F is not twice as warm as 10\(^{\circ}\)F. Accordingly, multiplication and division are not appropriate for these temperature scales. For example, 70\(^{\circ}\)C is not twice as warm as 35\(^{\circ}\)C. Just because data values are stored numerically, even with decimal digits, does not imply that those data values can be manipulated as numbers from the real number line with a fixed, non-arbitrary value of 0.
Working with data is distinct from a mathematician working with theoretical numbers. Working with data reveals four different representations of the values of continuous variables. We store the data on a computer system as a data file and then read the data into an analysis system, such as R or Python. As data analysts, we must ensure that the correct data type in our analysis corresponds to the correct conceptual definition of the variable.
Distinguish between four distinct representations of the values of a variable:
- Actual values as they exist apart from their measurement
- Data values as recorded measurements of the actual values
- Data values stored within a computer file in terms of bits, binary integers
- Data values as represented within the analysis system
Categorical Variables
The primary type of variable other than continuous variables is the categorical variable.
Categorical variable
Values of the variable are defined as a set of non-numerical categories called levels.
Examine the number of unique data values for each variable in the data frame. The values of a categorical variable form a relatively small number of categories called levels. Each level represents a distinct group. For example, the values of the categorical variable Gender define groups of Men, Women, and Other. Other categorical variables are Cola Preference, State of Residence, or Football Jersey Number. Yes, the number on the jersey consists of numeric digits, but those digits are labels, not subject to arithmetic operations such as computing an average. A categorical variable may also be called a qualitative variable or a grouping variable.
The values of categorical variables are labeled rather than measured. We do not measure the state of the USA in which a person resides but instead assign a person to that state based on self-report or an examination of public records. The classification into a group assigns a label, such as Oregon or Texas.
One categorical data type is a set of rankings, called ordinal data, which are data values that are ordered categories.
Ordinal data
Data values ordered by rank with unequal intervals that separate their values.
Suppose the top three sprinters are ranked in order of finish in the 100-meter dash: 1st, 2nd, and 3rd. The finish times represent a continuous variable, but simply ranking contestants by order of their finish does not convey if the race was extremely close or if the winner finished well ahead of their nearest competitor.
Ordinal data also results when the measured value of a continuous variable is so imprecise that, instead of a numerical scale, only a few categories exist in which the measured values can be placed. Suppose that persons admitted to the emergency room are swiftly placed into one of only three severity categories: mild, moderate, or severe. This simple rating scale recognizes that some injuries are more severe than others, but the severity is classified into one of only three categories. The underlying variable for Injury Severity is continuous. This underlying progression of severity is assumed, but not equal intervals of severity that separate the levels. The rater’s interpretation of Moderate Severity of Injury may be closer to Mild Severity than Severe Severity of Injury.
Another type of categorical data is classification into discrete, unordered categories.
Nominal data
Levels of a categorical variable with no natural order.
Data for Gender, State of Residence, and Phone Manufacturer are examples of nominal data.
Data Storage Types
How are the data values structured? Are the data values for a variable continuous or categorical, labels without numeric properties even if represented by integers? The data values for the variables are analyzed on the computer, so how the data values are conceptually defined should align with how the computer stores them.
After reading the data values into any data analysis app, verify that the data were read correctly and represented correctly in the resulting data frame before data analysis begins. Many things can go wrong. Perhaps errors occurred as the data values were entered into the data file. Maybe the data values were not correctly read into the data analysis app, such as R. For example, if numerical values contain $ signs or commas, the data values will be read as type character. There may be too much missing data to permit meaningful analysis.
Distinguish between the conceptual meaning of the variable’s data values and how they are stored on the computer.
Data storage type
How the data values of a variable are physically stored in the computer.
The data storage type is the computer’s representation of a data value in its binary memory locations. The storage type should match the conceptual definition of the variable.
Continuous Variables
Variables with numerical data values are the only variables that can represent continuous variables. However, some variables with numerical data values are categorical, so being numerical alone does not imply underlying continuity. R does not attempt to decide for the user if a numerical variable is continuous or categorical, a task that is often impossible to decide from the data values alone.
Categorical Variables
Categorical variables can have several different storage types. The two most common categorical storaage types are the same integer type for continuous variables and type character for variables with values of text, that is, alphanumeric characters.
The categories, the unique levels of the categorical variable, are its data values, either numeric digits, usually integers, or, text composed of alphabetical characters. For example, represent Gender numerically as 0 for Man, 1 for Woman, and 2 for Other. Or encode Gender with M, W, and O. Although the mnemonic coding with alphabetical characters better communicates meaning and prevents mistakes such as computing the mean of a column of 0’s, 1’s, and 2’s, both representations of categorical variables in the data are common.
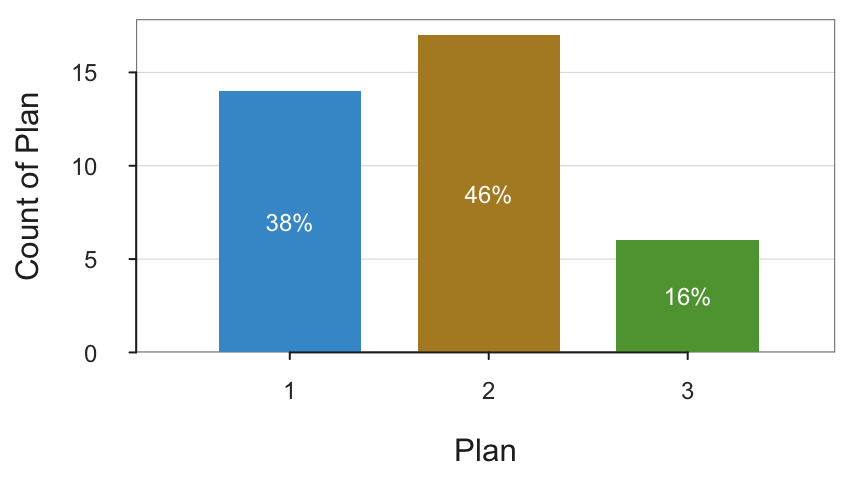
A potential confusion is that integer data values may represent categorical or numeric data. A categorical variable’s relatively small number of unique, non-numeric values can correspond to any data type. For example, in the data table from the Employee data file, the categorical variable Plan has three integer values – 1, 2, and 3 – corresponding to three health plans. Although the data values are numbers, in this context, they only serve as labels to define a categorical variable. They could be replaced with any other set of arbitrary labels, such as A, B, and C.
To avoid confusion, for at least two reasons it is better to represent categorical variables in the data with non-numeric values.
The meaning is clear for the values Man and Woman or M and W, such as in the Employee data table.
For Gender stored as an integer variable, does the 0 represent Man, Woman, or something else?A variable with non-numeric values has values that cannot be mistakenly treated as numeric values and then subjected to inappropriate numerical analysis.
There is no mean for the values of M and F, but there is for values encoded as 0, 1, and 2. Unfortunately, if this coding represents Gender, the mean is meaningless and misleading.
Implementation
Analyze Categorical Variables
Whether categorical variables are read into the data analysis system as integers or as text character strings, further adjustments are usually needed before analysis begins.
Categorical variables need more information than available from the data.
More information is typically required to analyze categorical variables than the data provides.
Three general issues for categorical variables may require answers before data analysis begins.
- For non-numeric data values, properly order the levels, such as Low, Medium, and High.
- Attach meaningful labels to the levels, particularly applicable to integer data values.
- Display potential response categories that did not occur in the data.
R: Analyze Categorical Variables - R Factors
Accept Existing Levels and Order
Suppose the data values for Gender present in a given data set are each one of two character strings: M or W. How should this variable be transformed for subsequent analysis to an R factor?
R: Analyze Categorical Variables - Accept Existing Levels and Order
Tableau: Analyze Categorical Variables - Accept Existing Levels and Order
Order Character String Levels
In the Employee data set, three levels describe the categorical variable JobSat: low, med, and high. Neither R nor Tableau knows the meaning of words such as “low”. These analysis systems choose some arbitrary ordering of the bars, an alphabetical ordering by default. Analyses that involve the unmodified JobSat variable, such as a bar chart, present the levels in the wrong order: high, low, and med.
R: Analyze Categorical Variables - Order Character String Levels
Tableau: Analyze Categorical Variables - Order Character String Levels
Label Integer Values
The levels of a categorical variable may be coded as integers. For example, for the employee data, the variable Plan is categorical, coded in the data file with the integers 1, 2, and 3 corresponding to three health plans, respectively named GoodHealth, GetWell, and BestCare. The corresponding bar graph necessarily displays these integer values, as illustrated with R/lessR.
The resulting visualizations are more meaningful with the output labeled with the names instead of integers, so transform a categorical variable read into a data frame as integers into a formal categorical variable with the corresponding labels.
R: Analyze Categorical Variables - Label Integer Values
Tableau: Analyze Categorical Variables - Label Integer Values
Add Levels Beyond the Data
Sometimes, not all possible responses for a categorical variable occur for one or more variables. The resulting visualization should usually include an analysis of potential responses for data that did not occur. To do so, the visualization procedures must be made aware of potential data values that do not exist in the data.
Suppose that an employee survey contained the following question:
For a small sample of 37 employees, no employee chose response Other. As a result, data visualizations such as a bar graph of the number of employees who responded to each category does not show the Other category. The correct bar graph would show all possible responses, and show a count of 0 for Other. How to visualize the full set of responses?
R: Analyze Categorical Variables - Add Levels Beyond the Data
Tableau: Analyze Categorical Variables - Add Levels Beyond the Data