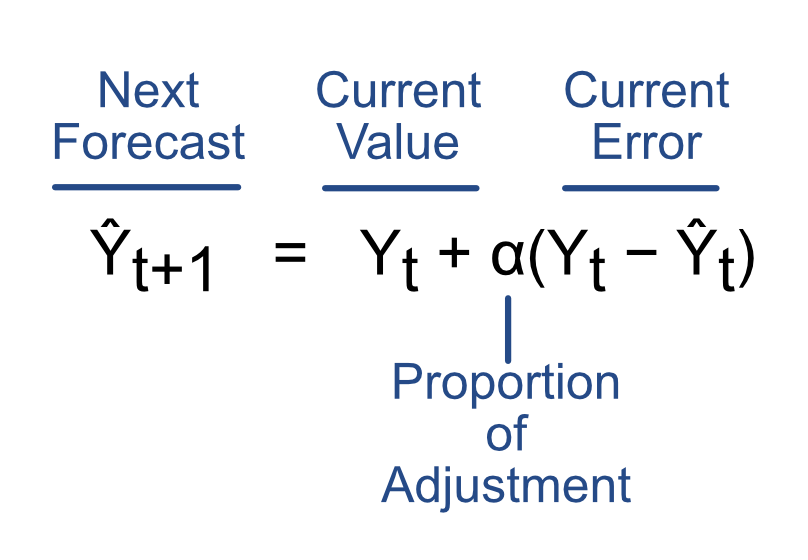
This week's focus is exponential smoothing of a time series, one of the most commonly used forecasting techniques. To forecast the value of the time series for the next time point, t+1, an exponential smoothing forecast self-adjusts from the forecasting error at the current time, t. Current forecast too large? Then lower the value of the next forecast. Current forecast too small? Then raise the value of the next forecast.
Compute the forecast, at Time t+1, as the current value of the time series, at Time t, plus some proportion of the error up or down that adjusts the forecast of the current value. This is the defining equation for exponential smoothing. The proportion of adjustment from the current forecasting error is called alpha, the smoothing factor, usually a number around 0.3 or less. A too-large value of alpha over adjusts to the random error component of the forecast. The larger the random error, the smaller should be the value of alpha.

However, the problem with limiting the forecast to the above equation is that it does not account for trend and seasonality. Further enhancements include a beta smoothing term to account for trend and a gamma smoothing term to account for seasonality. See the links below for more details.
online: Exponential Smoothing
video [15:51] Exponential Smoothing I: Concepts
video [20:26] Exponential Smoothing II: Implementation
video [4:31] Exponential Smoothing III: Seasonal Multiplicity