Research snippets
Support for research from NSF, AFOSR, DARPA, and Medtronic is
gratefully acknowledged.

|
Hybridization,
in the finite element context,
is the process of formulating methods exploiting
unknowns at the interfaces of mesh elements. Designing high order
methods with hybridization in mind has led to new families of methods
like the Hybridizable Discontinuous Galerkin (HDG) methods.
HDG methods were first introduced in our paper available
here.
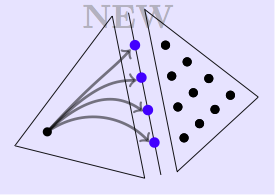
The basic difference in the design of a traditional discontinuous Galerkin (DG) method and an HDG method is a simple idea, pictorially illustrated aside. In traditional DG, a finite element node typically interacts with all nodes of an adjacent element. In contrast, in the HDG method it interacts only with interfacial nodes. This allows the elimination (or condensation) of all nodes, except the interfacial nodes, leading to a smaller global system, especially in the high order case. Although our initial motivation in designing the HDG method was to overcome the then-pervasive criticism that `DG methods have too many unknowns', a number of other fortuitous advantages arose, such as many vectorizable operations in the solution process, structured global matrices even on unstructured grids, fewer nonzeros in factored matrices, excellent compatibility with GPU architectures, flexible and transparent stabilization mechanism via an unconstrained stabilization parameter, sharp analytical tools, etc. |
| Rocket-triggered lightning is an often used technique in understanding when and how lightning occurs. (It is a technique whose roots can be traced back as early as Benjamin Franklin!) By controlled and reliably repeatable experiments, one hopes to understand the electrical field changes that accompany or trigger lightning. Working closely with electrical engineers performing these experiments we design tools to simulate the fields when lightning is triggered. For full details of the simulation shown aside, see our JGR paper. Way cooler pictures of real experiments are available at our collaborator's page. |

|
DPG schemes (discontinuous Petrov-Galerkin schemes) provide a framework to obtain extraordinarily stable methods for complex simulations. Below is a snippet from our first paper on a DPG scheme applied to the simulation of transport phenomena. A short set of lecture notes on DPG methods (including codes) are available for download.
| 
| 
|
|
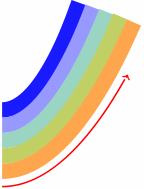
Pure transport does not mix materials across the
transport direction. This is indicated in the above
cartoon - the colors, representing material densities,
do not diffuse crosswind.
|
However most transport simulations unphysically diffuse materials crosswind.
Note how the colors diffuse horizontally
(crosswind) as we proceed upwards along the transport
direction in the above simulation (using a standard DG method).
|
In contrast, DPG methods, do not exhibit the
unphysical diffusion, as shown above. DPG methods
have an inherently different stability mechanism that
does not rely on any added artificial diffusion.
|
|
Photonic materials offer exciting possibilities for radical manipulation of light. Since their fabrication is challenging, mathematical predictions are valuable. Identification and calculation of localized defect modes in infinite periodic structures can be done by computing bandstructure diagrams. We developed finite elements for such computations (see our JCP paper). We also considered practical optical structures, which are, of course, finite and lossy, and therefore cannot have bandgaps. Yet, they can have resonances, which give valuable insight on how light can be manipulated. Resonance computations, like the one aside, pose significant numerical challenges, as described in our SIAP paper. |
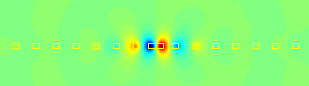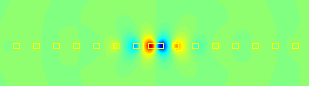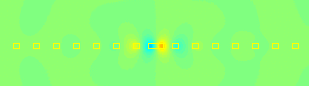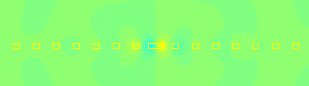
A computationally predicted trapped resonance mode |
|
Multigrid solvers are a class of numerical
techniques that can compute an approximate solution to certain
problems at asymptotically optimal computational cost. The optimal
complexity of multigrid has brought within the reach of simulation
many scientific problems previously thought to be of intractable
size. They are often best suited for solving systems arising from
discretizations of partial differential equations or integral
equations. They achieve their efficiency by cleverly utilizing a
multilevel heirarchy of discretization grids, together with certain
smoothing operations that are generally problem specific.
Identifying the classes of problems suitable for multigrid, designing appropriate multigrid algorithms suited for these problems, and proving their efficacy form a main theme of my research. This involves, in particular, proving convergence of multigrid iterations using techniques that heavily rely on the mathematical theory of partial differential equations and their discretizations. |
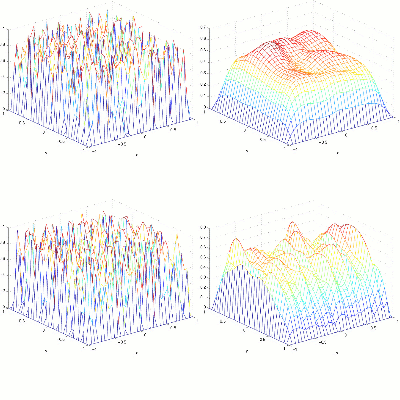
Why does Gauss-Seidel iteration smooth a random
function very well in most cases (as in the top row above),
while it only smooths directionally in some other cases
(bottom row)?
Download our multigrid
short course
prepared for participants of a Feb 2005 conference.
|
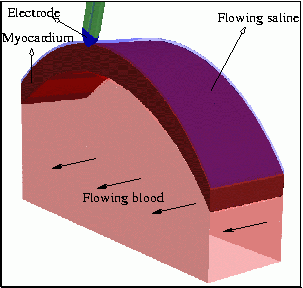
A part of the computational domain
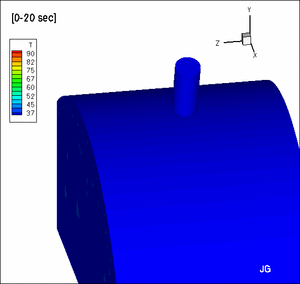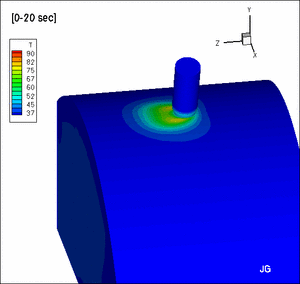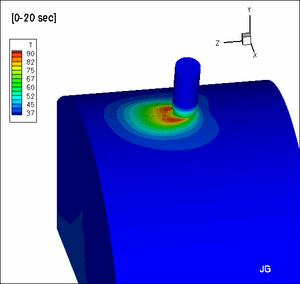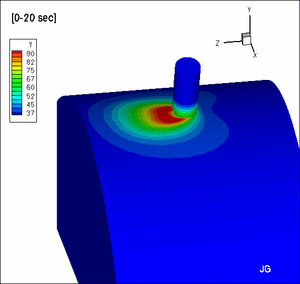
A computed solution showing that blood flow direction affects
the shape of ablation lesions
|
Ablation therapy is one of the
most commonly used treatment for arrhythmias. It prevents
irregular excitation of cardiac muscles by creating lesions
in regions where arrhythmias originate and propagate. The
number of reported ablation procedures in United States in
the year 2000 was about 15,000. A better understanding of
important parameters that affect lesion formation is not only
of importance to the bio-technology industry, but is also
critical to the well being of patients with arrhythmias.
Modern devices for ablation use saline irrigation to cool electrodes. To obtain successful computational models of such devices we must combine new modeling techniques with appropriate numerical methods. We developed a mathematical model for irrigated epicardial ablation based on a thin film approximation of saline flow irrigation (see our ABME paper online). Even with simplified models, fast and accurate numerical simulations require finite element techniques beyond the standard ones. |
For a press article on this work, see
SIAM News, September 2005, pp.2.